Evaluating performance is a crucial step in developing regression models. Because regression models return continuous outputs, such models allow for different gradations of right or wrong. Therefore, we measure the deviation between predictions and actual values in numerical terms. However, a universal metric to measure the performance of regression models does not exist. Instead, there are several metrics, each with its advantages and disadvantages. None of these metrics is sufficient alone, and it is often necessary to use them in combination. This article presents six regression error metrics and explains how to implement them in Python with Scikit-learn.
The rest of this article proceeds in two parts. The first part is conceptual and introduces six error metrics for measuring regression performance. We look at formulas and discuss their pros and cons. The discussion is summarized in a cheat sheet. The second part is a hands-on Python tutorial in which we generate synthetic time series data and use them for training a prediction model. Then we implement the six regression error metrics and evaluate the performance of our model.
Note that this article deals with regression errors. If you are looking for an overview of classification error metrics, check out this tutorial on classification error metrics.

Measuring Regression Errors
In general, we measure the performance of regression models by calculating the deviations between the predictions (y_pred) and the actual values (y_test). If the prediction value is below the actual value, the prediction error is positive. If the prediction lies above the real value, the prediction error is negative. However, in a sample of prediction values, the errors can vary greatly depending on the data point. Therefore, it is not enough to look at individual error values. Error metrics can inform us about the statistical distribution of errors in a prediction sample and, in this way, help us to measure the performance of regression models objectively.
Various metrics exist to measure regression errors. Each error metric can only cover a part of the overall picture. For instance, imagine you have developed a model to predict the consumption of a power plant. The model predictions are generally accurate, but the projections are wrong in a few cases. In other words, outliers among the prediction errors make it difficult to conclude the model performance. It is insufficient to calculate the average prediction error to understand this situation. Instead, a more robust measuring approach would combine different error metrics to conclude the probability that prediction errors lie within a specific range.
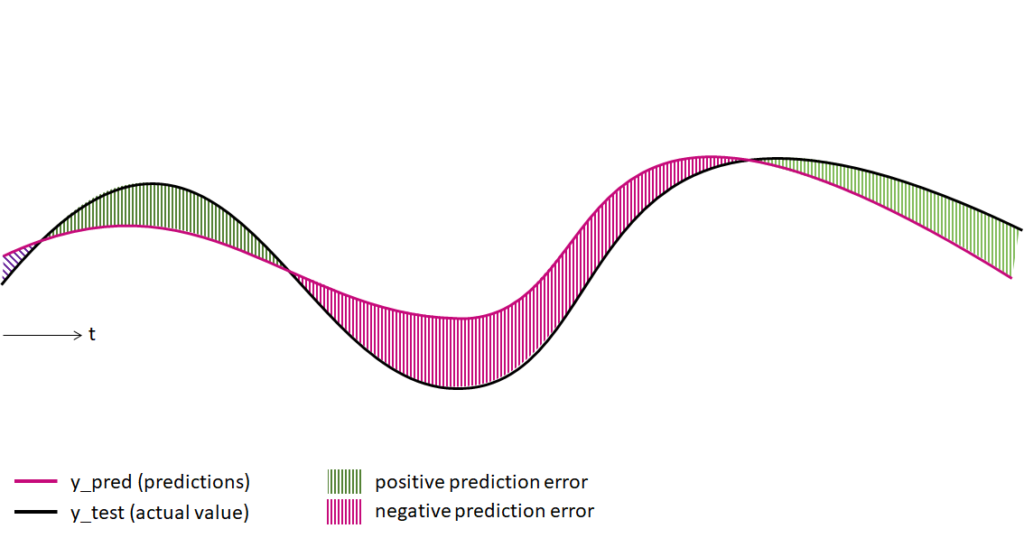
Six Error Metrics for Measuring Regression Errors
The following six metrics help measure prediction errors. We can apply them to various regression problems, including time series forecasting.
- Mean Absolute Error (MAE)
- Mean Absolute Percentage Error (MAPE)
- Median Absolute Error (MedAE)
- Mean Squared Error (MSE)
- Root Mean Squared Error (RMSE)
- Median Absolute Percent Error (MdAPE)
Mean Absolute Error (MAE)
Mean Absolute Error (MAE) is a metric commonly used to measure the arithmetic average of deviations between predictions and actual values.
An MAE of “5” tells us that, on average, our predictions deviate from the actual values by 5. Whether this error is considered small or large will depend on the application case and the scale of the predictions. For instance, 5 nanometers in the case of a building might be small, but if it’s five nanometers in the case of a biological membrane, it might be significant. So when working with the MAE, mind the scale.
- It is scale-dependent
- The MAE considers the absolute values to take both positive and negative deviations from the actual.
- The MAE is sensitive to outliers, as large values can substantially impact. For this reason, we should use the MAE in combination with additional metrics.
- The MAE shares the same unit with the predictions.
Mean Absolute Percentage Error (MAPE)
The mean absolute percentage error calculates the mean percentage deviation between predictions and actual values.
- The mean absolute percentage error is scale-independent, making it easier to interpret.
- We must not use the MAPE whenever a single value is zero
- The MAPE puts a heavier penalty on negative errors
Mean Squared Error (MSE)
We can calculate the MSE by measuring the average squares of the differences between the estimated and actual values.
- Since all values are squared, the MSE is very sensitive to outliers.
- An MSE much larger than the MAE indicates strong outliers among the prediction errors. The formula of the MSE is:
Median Absolute Error (MedAE)
The Median Absolute Error (MedAE) calculates the median deviation between predictions and actual values.
- The MedAE has the same unit as the predictions.
- A MedAE of value 10 means that 50% of the errors are greater than 10 and 50% are below this value.
- The MedAE is resistant to outliers. Therefore, we often use it in combination with the MAE. A substantial deviation between MAE and MedAE is an indication that there are outliers among the errors. In other words, the prediction model deviates more from the actual value than on average.
Root Mean Squared Error (RMSE)
The root-mean-squared error is another standard way to measure the performance of a forecasting model.
- Has the same unit as the predictions
- A good measure of how accurately the model predicts the response
- Robust to outliers
Median Absolute Percentage Error (MdAPE)
The median absolute percentage error (MdAPE) measures the accuracy of a prediction model. It is similar to the median absolute percentage error but, as the name implies, calculates the median error for a set of forecasts. As a result, the MdAPE is more resilient to outliers than the MAPE. However, it is also less intuitive. A MdAPE of 5% means that half of the absolute percentage errors are less than 5%, and half are over 5%.
- Scale-dependent
- Not to be used whenever a single value is zero.
- More robust to distortion from outliers than the MAPE
Regression Error Cheat Sheet
The cheat sheet provides an overview of the six regression error metrics. It contains the mathematical formula for each regression metric, a short code sequence to implement in Python, and some hints for their interpretation.
Implementing Regression Error Metrics in Python: Time Series Prediction Example
Now that we have familiarized ourselves with standard regression error metrics, it’s time to see them in action. In the following, we will develop and test a regression model in Python. We begin by generating some synthetic time series data. Subsequently, we use the data to train a simple regression model based on a Keras neural network. The model will try to continue the time series and predicts a continious value for the next time step. We will use this model to predict a test dataset and measure the prediction performance using the error metrics.
The code of this Python example is available on the GitHub repository.
Prerequisites
Before starting the coding part, make sure that you have set up your Python 3 environment and required packages. If you don’t have an environment yet, you can follow the steps in this tutorial to set up the Anaconda environment.
Also, make sure you install all required packages. In this tutorial, we will be working with the following standard packages:
In addition, we will be using Keras (2.0 or higher) with Tensorflow backend and the machine learning library scikit-learn.
You can install packages using console commands:
- pip install <package name>
- conda install <package name> (if you are using the anaconda packet manager)
Step #1 Generate Synthetic Time Series Data
We begin by generating synthetic time series data. The script below creates the time series by multiplying different sine curves.
# A tutorial for this file is available at www.relataly.com
import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from tensorflow.keras.models import Sequential
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.layers import LSTM, Dense
import seaborn as sns
sns.set_style('white', { 'axes.spines.right': False, 'axes.spines.top': False})
# Creating the sample sinus curve dataset
steps = 1000; gradient = 0.002
list_a = []
for i in range(0, steps, 1):
y = 100 * round(math.sin(math.pi * i * 0.02 + 0.01), 4) * round(math.sin(math.pi * i * 0.005 + 0.01), 4) * round(math.sin(math.pi * i * 0.005 + 0.01), 4)
list_a.append(y)
df = pd.DataFrame({"valid": list_a}, columns=["valid"])
# Visualizing the data
fig, ax1 = plt.subplots(figsize=(16, 4))
sns.lineplot(data=df)
ax1.xaxis.set_major_locator(plt.MaxNLocator(30))
plt.title("sine curve data")
Step #2 Data Preparation
Now that we have the synthetic data available, we can prepare it as inputs for training our regression model. Running the following code will scale and split the data and bring it into a shape that we can use as input batches to a neural network.
# Feature Selection - Only Close Data
train_df = df.copy()
data_unscaled = df.values
# Transform features by scaling each feature to a range between 0 and 1
mmscaler = MinMaxScaler(feature_range=(0, 1))
np_data = mmscaler.fit_transform(data_unscaled)
# Set the sequence length - this is the timeframe used to make a single prediction
sequence_length = 15
# Prediction Index
index_Close = 0
# Split the training data into train and train data sets
# As a first step, we get the number of rows to train the model on 80%% of the data
train_data_length = math.ceil(np_data.shape[0] * 0.8)
# Create the training and test data
train_data = np_data[0:train_data_length, :]
test_data = np_data[train_data_length - sequence_length:, :]
# The RNN needs data with the format of [samples, time steps, features]
# Here, we create N samples, sequence_length time steps per sample, and 6 features
def partition_dataset(sequence_length, train_df):
x, y = [], []
data_len = train_df.shape[0]
for i in range(sequence_length, data_len):
x.append(train_df[i-sequence_length:i,:]) #contains sequence_length values 0-sequence_length * columsn
y.append(train_df[i, index_Close]) #contains the prediction values for validation (3rd column = Close), for single-step prediction
# Convert the x and y to numpy arrays
x = np.array(x)
y = np.array(y)
return x, y
# Generate training data and test data
x_train, y_train = partition_dataset(sequence_length, train_data)
x_test, y_test = partition_dataset(sequence_length, test_data)
# Print the shapes: the result is: (rows, training_sequence, features) (prediction value, )
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
# Validate that the prediction value and the input match up
# The last close price of the second input sample should equal the first prediction value
print(x_test[1][sequence_length-1][index_Close])
print(y_test[0])
Out: x_tain.shape: (584, 15, 1) -- y_tain.shape: (584,)
Step #3 Training a Time Series Regression Model
Once we have prepared the data, we can train the regression model. Our model uses a simple neural network architecture. Running the code below defines the model architecture and compiles the model.
# Settings batch_size = 5 epochs = 4 n_features = 1 # Configure and compile the neural network model # The number of input neurons is defined by the sequence length multiplied by the number of features lstm_neuron_number = sequence_length * n_features # Create the model model = Sequential() model.add(LSTM(lstm_neuron_number, return_sequences=False, input_shape=(x_train.shape[1], 1)) ) model.add(Dense(1)) model.compile(optimizer="adam", loss="mean_squared_error") # Train the model history = model.fit(x_train, y_train, batch_size=batch_size, epochs=epochs)
Epoch 1/4 584/584 [==============================] - 1s 2ms/step - loss: 0.1047 Epoch 2/4 584/584 [==============================] - 1s 1ms/step - loss: 0.0153 Epoch 3/4 584/584 [==============================] - 1s 1ms/step - loss: 0.0102 Epoch 4/4 584/584 [==============================] - 1s 1ms/step - loss: 0.0064
Now that the model architecture is defined, you can run the code below to initiate the training process.
# Settings batch_size = 5 # Train the model history = model.fit(x_train, y_train, batch_size=batch_size, epochs=epochs)
Step #4 Making Test Predictions
Let’s see how good or bad our model performs. We will make predictions on our test dataset by running the code below. We store the results in a new DataFrame called “predictions.”
# Get the predicted values y_pred_scaled = model.predict(x_test) y_pred = mmscaler.inverse_transform(y_pred_scaled) y_test_unscaled = mmscaler.inverse_transform(y_test.reshape(-1, 1))
Next, we want to get an idea of how our model performs. We, therefore, create a line plot that shows the predictions and the actual values of the time series. We colorize the differences between predictions and actual values to highlight the prediction errors.
# Create the line plot
test_df = pd.DataFrame({'y_test': y_test_unscaled.flatten(), 'y_pred': y_pred.flatten()})
fig, ax1 = plt.subplots(figsize=(16, 8), sharex=True)
sns.lineplot(data=test_df)
ax1.tick_params(axis="x", rotation=0, labelsize=10, length=0)
plt.title("y_pred vs y_test Truth")
plt.legend(["y_pred", "y_test"], loc="upper left")
# Fill between plotlines
mpl.rc('hatch', color='k', linewidth=2)
ax1.fill_between(test_df.index, test_df["y_test"], test_df["y_pred"], facecolor = 'white', alpha=.9)
plt.show()
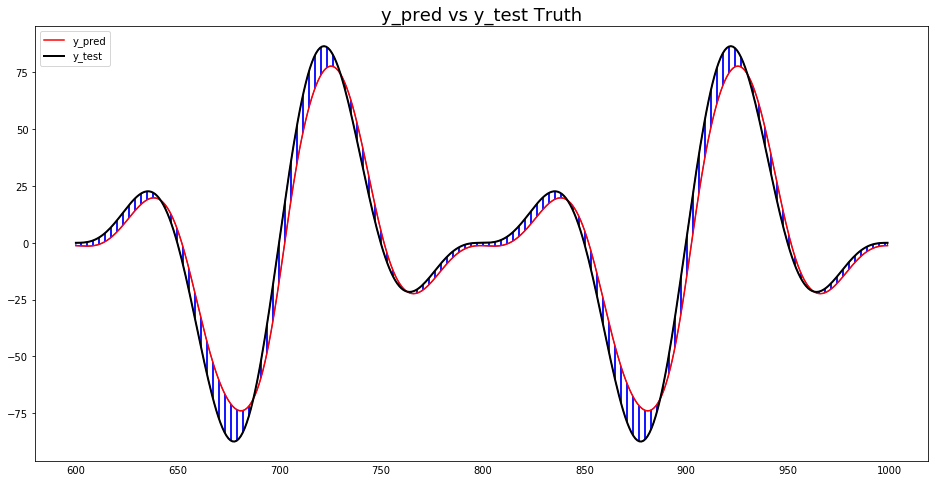
The plot shows that the prediction errors vary and are sometimes positive and sometimes negative.
Step #5 Calculating the Regression Error Metrics: Implementation and Evaluation
Now that we have predicted the test set, we calculate the six regression error metrics. In most cases, you won’t have to use all six regression error metrics to understand how well a model performs. In most cases, it is sufficient to use a combination of two or three of them.
# Mean Absolute Error (MAE)
MAE = np.mean(abs(y_pred - y_test_unscaled))
print('Mean Absolute Error (MAE): ' + str(np.round(MAE, 2)))
# Median Absolute Error (MedAE)
MEDAE = np.median(abs(y_pred - y_test_unscaled))
print('Median Absolute Error (MedAE): ' + str(np.round(MEDAE, 2)))
# Mean Squared Error (MSE)
MSE = np.square(np.subtract(y_pred, y_test_unscaled)).mean()
print('Mean Squared Error (MSE): ' + str(np.round(MSE, 2)))
# Root Mean Squarred Error (RMSE)
RMSE = np.sqrt(np.mean(np.square(y_pred - y_test_unscaled)))
print('Root Mean Squared Error (RMSE): ' + str(np.round(RMSE, 2)))
# Mean Absolute Percentage Error (MAPE)
MAPE = np.mean((np.abs(np.subtract(y_test_unscaled, y_pred)/ y_test_unscaled))) * 100
print('Mean Absolute Percentage Error (MAPE): ' + str(np.round(MAPE, 2)) + ' %%')
# Median Absolute Percentage Error (MDAPE)
MDAPE = np.median((np.abs(np.subtract(y_test_unscaled, y_pred)/ y_test_unscaled))) * 100
print('Median Absolute Percentage Error (MDAPE): ' + str(np.round(MDAPE, 2)) + ' %%')
Mean Absolute Error (MAE): 6.95 Median Absolute Error (MedAE): 5.05 Mean Squared Error (MSE): 78.7 Root Mean Squared Error (RMSE): 8.87 Mean Absolute Percentage Error (MAPE): 10339.13 %% Median Absolute Percentage Error (MDAPE): 26.8 %%
Step #6 Interpreting the Regression Error Metrics
Let’s look at the regression error metrics, starting with the MAE and the MedAE. The MAE is 6.95, and the MedAE is 5.05. These values are close, indicating that our prediction errors are equally distributed but might include some outliers.
To better understand possible outliers, we look at the MSE. With a value of 78.7, the MAE is a little bit higher than the square of the MAE. The RMSE is slightly higher than the MAE, which is another indication that the prediction errors lie in a narrow range.
How much deviate the predictions of our model from the actual values in percentage terms? The MAPE is typically used as a starting point to answer this question. With 10339.13 percent, it is exceptionally high. So is our model very much mistaken? The answer is no – the MAPE is misleading. The problem is that several actual values are close to zero, e.g., 0.00001. While the predictions of our model are close to the actual values in absolute numbers, the MAPE divides the residual values by the actual values, e.g., 0.000001, and sums them up. Thus the MAPE becomes very large.
The Median of the MDAPE is 26.8%. So, 50% of our forecasting errors are higher than 26.8%, and 50% are lower. Consequently, we can assume that when our model makes a prediction, the probability that the deviation is 26.8% from the actual value is 50% – that is not as terrible as the MAPE would indicate. The plotlines of the predictions and actual values support these findings.
Summary
This article has presented six error metrics for evaluating regression errors. Remember that none of these metrics alone is sufficient to evaluate a model’s performance. Instead, we should use a combination of multiple metrics. We have discussed the advantages and disadvantages of the metrics. In the second part of this tutorial, we implemented a time series regression example. After training an exemplary regression model, we used the six regression metrics to evaluate the model performance.
It’s important to remember that different error metrics are suitable for different types of regression problems. For example, mean absolute error (MAE) is a good choice when you want to know how close the predictions are to the true values, but it is not very sensitive to large errors. Root mean squared error (RMSE) is a more sensitive metric that punishes large errors more heavily, but it can be difficult to interpret because it is in the same units as the original data.
I hope this article was helpful. If you have any remarks or questions remaining, write them in the comments.
Sources and Further Reading
The links above to Amazon are affiliate links. By buying through these links, you support the Relataly.com blog and help to cover the hosting costs. Using the links does not affect the price.



Another well explianed content. Thank yo for always. Can we basically conclude that the lower all the values for the metrics are the better? Especially the Median Absolute Percentage Error (MDAPE)
Hi Olaitan, thanks for your message. Yes, in general you can say for all common regression metrics, the lower the better.