Embark on a journey into the world of unsupervised machine learning with this beginner-friendly Python tutorial focusing on K-Means clustering, a powerful technique used to group similar data points into distinct clusters. This invaluable tool helps us make sense of complex datasets, finding hidden patterns and associations without the need for a predetermined target variable. This comes in handy, especially when dealing with data whose similarities and differences aren’t immediately apparent.
Divided into two insightful sections, this blog post first delves into the theoretical foundation of the K-Means clustering algorithm. We’ll explore its real-world applications, its strengths, and its weaknesses, providing a comprehensive overview of what makes K-Means an essential tool in any data scientist’s toolkit.
In the second part of the blog, we switch gears and dive into a hands-on Python tutorial. Here, we’ll walk you through a practical example of K-Means clustering, using it to uncover three distinct spherical clusters within a synthetic dataset. To round up, we’ll put our model to the test, using it to predict clusters within a test dataset, and then we’ll visualize the results for easy understanding.
Whether you’re a seasoned data scientist or a beginner looking to dip your toes into the field, this blog post offers a simple and accessible introduction to cluster engineering with K-Means in Python. Follow along, and uncover the hidden potential of your data today!

Findings Clusters in Multivariate Data with k-Means
K-Means clustering is a prominent unsupervised machine learning algorithm utilized to partition datasets into a predefined number (‘k’) of distinct clusters, each brimming with similar data points. To begin, the algorithm identifies ‘k’ random data points which serve as the initial centroids – the central points representing each cluster. It then proceeds in an iterative fashion, continuously reassigning each data point to the centroid nearest to it, followed by updating each centroid to the average of the data points assigned to its cluster. This process repeats until the centroids no longer change positions or until a set maximum number of iterations is reached.
The underlying objective of the K-Means algorithm is to minimize the within-cluster sum of squares (WCSS), a metric indicating the cumulative distance between each data point within a cluster and its corresponding centroid. By reducing the WCSS, K-Means aims to form the most compact and clearly separable clusters.
The K-Means algorithm has garnered substantial popularity in the field of data science for its speed and simplicity in implementation. However, it isn’t without its limitations. It requires the number of clusters to be specified beforehand and operates under the assumption that all clusters are spherical and uniformly sized. In the following sections, we’ll delve into the intricacies of this powerful yet straightforward algorithm and discuss its use in real-world applications.
Understanding the Mechanics of K-Means Clustering Algorithm
At its core, K-Means clustering is a dynamic algorithm designed to simplify complex data patterns. This machine learning model is a champion of unsupervised learning, adept at grouping similar data points into a predetermined number (‘k’) of unique clusters.
Starting the process, the K-Means algorithm selects ‘k’ random data points, which act as the initial centroids or the central figures of the clusters. The algorithm then goes through a series of iterative steps, continually allocating each data point to its closest centroid, and recalibrating the centroid to be the mean of all data points that are assigned to its cluster. This cycle repeats until we achieve stable centroids, i.e., they stop moving, or until a pre-set maximum number of iterations is completed.
The fundamental goal of K-Means lies in minimizing the within-cluster sum of squares (WCSS). This term refers to the sum of the distances of each data point in a cluster to its centroid. By lowering WCSS, K-Means strives to construct compact clusters that are distinctly separate from each other.
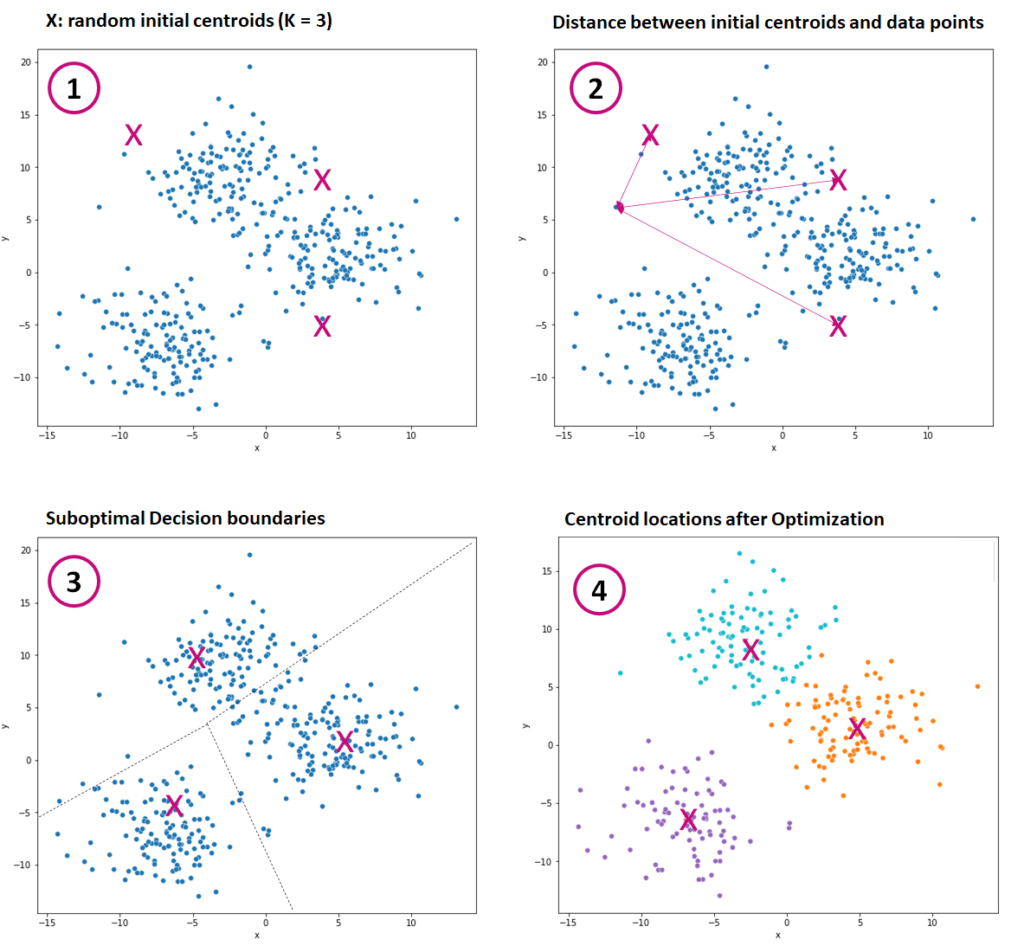
In the illustration below, we assume a cluster with three cluster centers. K-Means carries out several steps to partition the data.
- Initially, the algorithm k chooses random starting positions for the centroids. Alternatively, we can also position the centroids manually.
- Then the algorithm calculates the distance between the data points and the three centroids. The data points are assigned to the closest centroid/cluster where the cluster variance increases the least.
- Next, the algorithm calculates the Euclidean distance between the centroids and their assigned data points. The result is linear decision boundaries that separate the clusters but are not yet optimal.
- From then on, the algorithm optimizes the centroids’ positions to lower the resulting clusters’ variance. Then, the previous steps are repeated: averaging, assigning the data points to clusters, and shifting the centroids.
The process ends when the positions of the centroids do not change anymore.
How many Clusters?
A particular challenge is that k-means requires estimating the number of clusters k. When tackling new clustering problems, we usually don’t know the optimal number of clusters. Unless the data is not too complex, we can often estimate the number of centers by looking at one or more scatter plots. However, this approach only works when the data has a few dimensions. For complex data with many dimensions, it is common to experiment with varying numbers of k to find an appropriate size for the problem. We can automate this process using hyperparameter tuning techniques such as grid search or random search. The idea is to try out different cluster sizes and identify the size that best differentiates between clusters.
Pros and Cons of k-Means Clustering
Although K-Means is esteemed for its swift operation and uncomplicated implementation, it comes with a set of constraints. We need to know the strengths and weaknesses of clustering techniques such as k-Means. In general, clustering can reveal structures and relationships in data supervised machine learning methods like classification likely would not uncover. In particular, when we suspect different subgroups in the data that differ in their behavior, clustering can help discover what makes these groups unique.
K-Means, in particular, possesses a unique ability to detect and segregate spherical-shaped clusters efficiently. However, its performance may falter when faced with clusters embodying more intricate structures like half-moons or circles, often struggling to differentiate them accurately.
Another potential limitation of K-Means lies in its prerequisite of specifying the number of clusters in advance. This requirement can prove challenging when the true number of clusters within a dataset is unknown or ambiguous. In such scenarios, alternative clustering techniques, such as affinity propagation or hierarchical clustering, might be more suitable, as they possess the ability to automatically determine the optimal number of clusters.
Applications of Clustering
The k-means algorithm is used in a variety of applications, including the following:
- A typical use case for clustering is in marketing and market segmentation. Here clustering is used to identify meaningful segments of similar customers. The similarity can be based on demographic data (age, gender, etc.) or customer behavior (for example, the time and amount of a purchase).
- Medical research uses clustering to divide patient groups into different subgroups, for example, to assess stroke risk. After clustering, the next step is to develop separate prediction models for the subgroups to estimate the risk more accurately.
- An application in the financial sector is outlier detection in fraud detection. Banks and credit card companies use clustering to detect unusual transactions and flag them for verification.
- Spam filtering: The input data are attributes of emails (text length, words contained, etc.) and help separate spam from non-spam emails.
Implementing a K-Means Clustering Model in Python
In the following, we run a cluster analysis on synthetic data using Python and scikit-learn. We aim to train a K-Means cluster model in Python that distinguishes three clusters in the data. Given that the data is synthetic, we’re already privy to which cluster each data point pertains to. This foreknowledge enables us to evaluate the performance of our model post-training, gauging how effectively it can differentiate between the three predefined clusters.
The code is available on the GitHub repository.
Prerequisites
Before beginning the coding part, make sure that you have set up your Python 3 environment and required packages. If you don’t have an environment, consider the Anaconda Python environment. To set it up, you can follow the steps in this tutorial.
Also, make sure you install all required packages. In this tutorial, we will be working with the following standard packages:
This article uses the k-means clustering algorithm from the Python library Scikit-learn. We also use Seaborn for visualization.
You can install these libraries using console commands:
- pip install <package name>
- conda install <package name> (if you are using the anaconda packet manager)
Step #1: Generate Synthetic Data
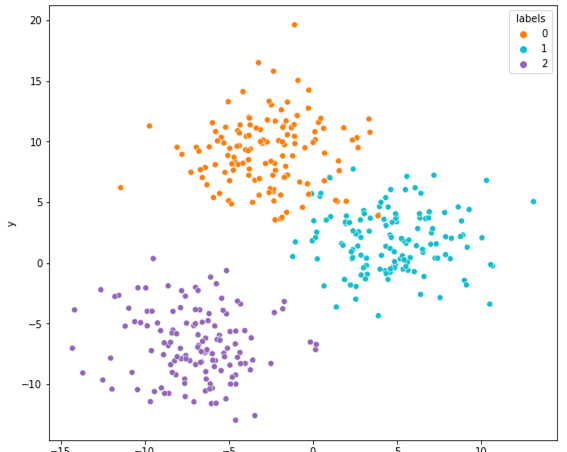
We start with the generation of synthetic data. For this purpose, we use the make_blobs function from the scikit-learn library. The function generates random clusters in two dimensions spherically arranged around a center. In addition, the data contains the respective cluster to which the data points belong. We use a scatterplot to visualize the data.
import pandas as pd
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split as train_test_split
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report, confusion_matrix
# Generate synthetic data
features, labels = make_blobs(
n_samples=400,
centers=3,
cluster_std=2.75,
random_state=42
)
# Visualize the data in scatterplots
def scatter_plots(df, palette):
fig, ax = plt.subplots(nrows=1, ncols=2, sharex=True, figsize=(20, 8))
fig.subplots_adjust(hspace=0.5, wspace=0.2)
ax1 = plt.subplot(1,2,1)
sns.scatterplot(ax = ax1, data=df, x='x', y='y', hue= 'labels', palette=palette)
plt.title('Clusters')
ax2 = plt.subplot(1,2,2)
sns.scatterplot(ax = ax2, data=df, x='x', y='y')
plt.title('How the model sees the data during training')
palette = {1:"tab:cyan",0:"tab:orange", 2:"tab:purple"}
df = pd.DataFrame(features, columns=['x', 'y'])
df['labels'] = labels
scatter_plots(df, palette)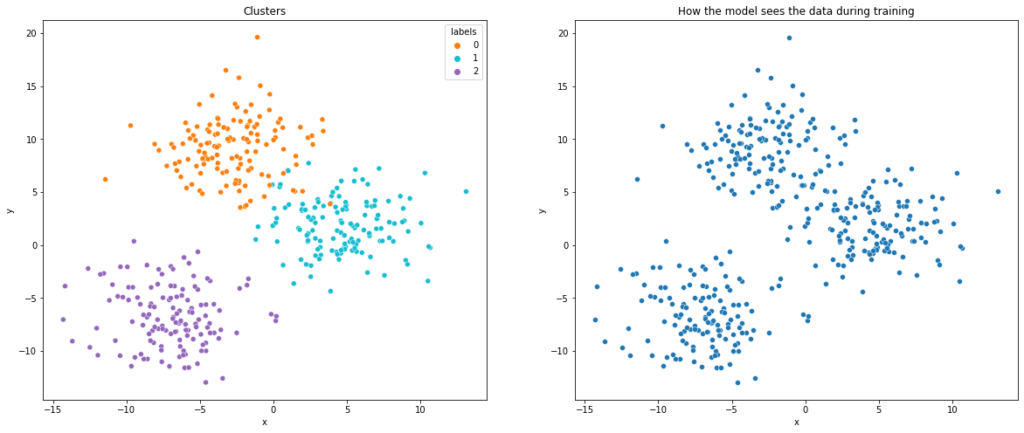
Step #2: Preprocessing
There are some general things to keep in mind when preparing data for use with K-Means clustering:
- Missing data and outliers: if we have missing entries in our data, we need to handle these, for example, by removing the records or filling the missing values with a mean or median. In addition, K-means is sensitive to outliers. Therefore, make sure that you eliminate outliers from the training data.
- Normalization: K-Means can only deal with integer values. So, either we map the categorical variables to integer values or use one-hot-encoding to create separate binary variables.
- Dimensionality reduction: In general, having too many variables in a dataset can negatively affect the performance of clustering algorithms. A good practice is to keep the number of variables below 30, for example, by using techniques for dimensionality reduction such as Principal-Component-Analysis.
- Scaling: Important to note is also that K-means require scaling the data.
Our synthetic dataset is free of outliers or missing values. Therefore, we only need to scale the data. In addition, we separate the class labels of the clusters from the training set and split the data into a train- and a test dataset.
# Scale the data scaler = StandardScaler() scaled_features = scaler.fit_transform(features) X = scaled_features #Training data y = labels #Prediction label # Split the data into x_train and y_train data sets X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, random_state=0)
Step #3: Train a k-Means Clustering Model
Once we have prepared the data, we can begin the cluster analysis by training a K-means model. Our model uses the k-means algorithm from Python scikit-learn library. We have various options to configure the clustering process:
- n_clusters: The number of clusters we expect in the data.
- n_init: The number of iterations k-means will run with different initial centroids. The algorithm returns the best model.
- max_iter: The max number of iterations for a single run
We expect three clusters and configure the algorithm to run ten iterations.
# Create a k-means model with n clusters
kmeans = KMeans(
init="random",
n_clusters=3,
n_init=10,
max_iter=300,
random_state=42
)
# fit the model
kmeans.fit(X_train)
print(f'Converged after {kmeans.n_iter_} iterations')Converged after 4 iterations
Our model has already converged after four iterations. Next, we will look at the results.
Step #4: Make and Visualize Predictions
Next, we’ll be delving into the practical aspect of our Python tutorial by analyzing the performance of our trained K-Means model using synthetic data.
In the following Python code, we:
- Extract the cluster centers from the trained K-Means model and unscale them.
- Add the predicted and actual labels to our unscaled training data.
- Define a function,
scatter_plots(), that creates two scatter plots: one for the predicted labels and another for the actual labels. - Call this function, passing the training data, cluster centers, and a color palette as arguments.
Please note:
- We use a dictionary as a color palette to differentiate between clusters.
- The colors between the two plots may not match due to K-Means assigning numbers to clusters without prior knowledge of initial labels.
# Get the cluster centers from the trained K-means model
cluster_center = scaler.inverse_transform(kmeans.cluster_centers_)
df_cluster_centers = pd.DataFrame(cluster_center, columns=['x', 'y'])
# Unscale the predictions
X_train_unscaled = scaler.inverse_transform(X_train)
df_train = pd.DataFrame(X_train_unscaled, columns=['x', 'y'])
df_train['pred_label'] = kmeans.labels_
df_train['true_label'] = y_train
def scatter_plots(df, cc, palette):
fig, ax = plt.subplots(nrows=1, ncols=2, sharex=True, figsize=(20, 8))
fig.subplots_adjust(hspace=0.5, wspace=0.2)
# Print the predictions
ax2 = plt.subplot(1,2,1)
sns.scatterplot(ax = ax2, data=df, x='x', y='y', hue='pred_label', palette=palette)
sns.scatterplot(ax = ax2, data=cc, x='x', y='y', color='r', marker="X")
plt.title('Predicted Labels')
# Print the actual values
ax1 = plt.subplot(1,2,2)
sns.scatterplot(ax = ax1, data=df, x='x', y='y', hue= 'true_label', palette=palette)
sns.scatterplot(ax = ax1, data=cc, x='x', y='y', color='r', marker="X")
plt.title('Actual Labels')
# The colors between the two plots may not match.
# This is because K-means does not know the initial labels and assigns numbers to clusters
palette = {1:"tab:cyan",0:"tab:orange", 2:"tab:purple"}
scatter_plots(df_train, df_cluster_centers, palette)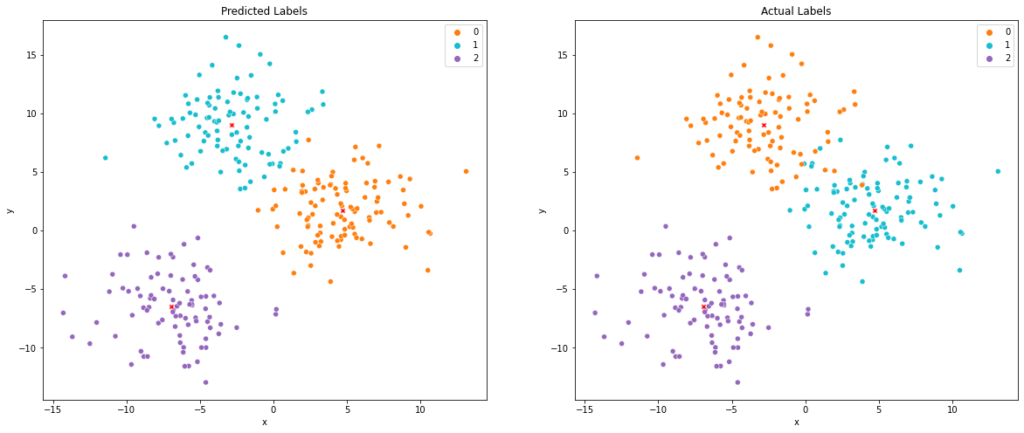
The scatterplot above shows that K-Means found the three clusters. As a side note, the colors between the two plots do not match because K-means does not know the initial labels and assigns numbers to clusters.
Step #5: Measuring Model Performance
Next, we measure the performance of our clustering model. K-means is an unsupervised machine learning algorithm, which means that it is used to cluster data points into groups based on their similarity, without the use of labeled training data. However, we can compare the cluster assignments to the labels attached to the data and see if the model can predict them correctly. In this way, we can use traditional classification metrics such as accuracy and f1_score to measure the performance of our clustering model.
First, we unify the cluster labels as A, B, and C.
# The predictive model has the labels 0 and 1 reversed. We will correct that first.
#df_train['pred_test'] = df_train['pred_labels'].map({2:2, 1:3, 0:1})
df_eval = df_train.copy()
df_eval['true_label'] = df_eval['true_label'].map({0:'A', 1:'B', 2:'C'})
df_eval['pred_label'] = df_eval['pred_label'].map({0:'B', 1:'A', 2:'C'})
df_eval.head(10)x y pred_label true_label 0 -9.007547 -10.302910 C C 1 1.009238 7.009681 A B 2 -6.565501 -6.466780 C C 3 2.389772 7.727235 B B 4 -5.422666 -2.915796 C C 5 -12.024305 -7.846772 C C 6 -4.006250 9.319323 A A 7 -6.297788 6.435267 A A 8 2.169238 3.325947 B B 9 -5.140506 -4.205585 C C
It is a common practice to create scatterplots on the predictions to visually verify the quality of the clusters and their decision boundaries. The following scatter plot shows the correctly assigned values and where our model was wrong.
# Scatterplot on correctly and falsely classified values df_eval.loc[df_eval['pred_label'] == df_eval['true_label'], 'Correctly classified?'] = 'True' df_eval.loc[df_eval['pred_label'] != df_eval['true_label'], 'Correctly classified?'] = 'False' plt.rcParams["figure.figsize"] = (10,8) sns.scatterplot(data=df_eval, x='x', y='y', color='r', hue='Correctly classified?')
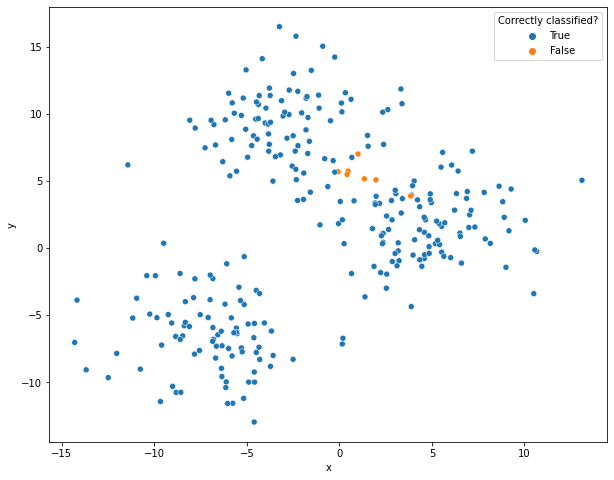
The K-Means model correctly assigned most data points (blue) to their actual cluster. The few misclassified points are located at a decision boundary between two clusters (marked in orange).
# Create a confusion matrix
def evaluate_results(model, y_true, y_pred, class_names):
tick_marks = [0.5, 1.5, 2.5]
# Print the Confusion Matrix
fig, ax = plt.subplots(figsize=(10, 6))
results_log = classification_report(y_true, y_pred, target_names=class_names, output_dict=True)
results_df_log = pd.DataFrame(results_log).transpose()
matrix = confusion_matrix(y_true, y_pred)
model_score = score(y_pred, y_true, average='macro')
sns.heatmap(pd.DataFrame(matrix), annot=True, fmt="d", linewidths=.5, cmap="YlGnBu")
plt.xlabel('Predicted label'); plt.ylabel('Actual label')
plt.title('Confusion Matrix on the Test Data')
plt.yticks(tick_marks, class_names); plt.xticks(tick_marks, class_names)
print(results_df_log)
y_true = df_eval['true_label']
y_pred = df_eval['pred_label']
class_names = ['A', 'B', 'C']
evaluate_results(kmeans, y_true, y_pred, class_names)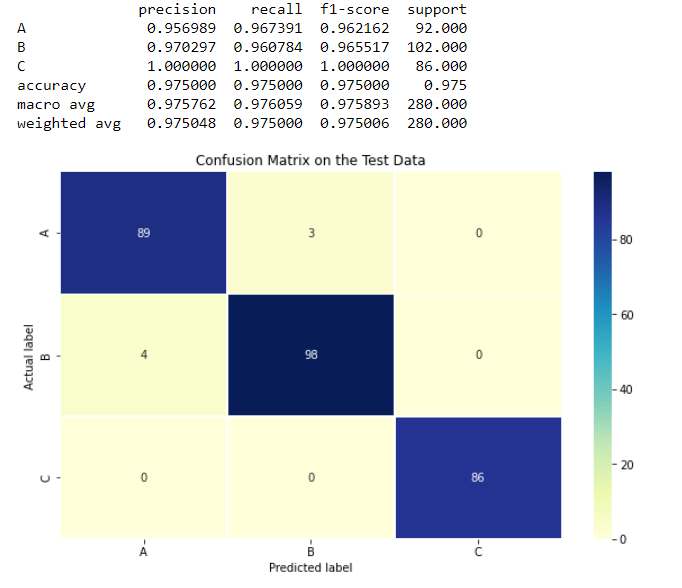
As we can see, the model has done a good job of grouping the labels into the attached classes.
Summary
algorithm, capable of parsing intricate datasets into discrete, non-overlapping clusters. With this guide, you should have a clear understanding of how this algorithm operates, as well as its unique strengths and potential limitations. Remember, k-Means excels when dealing with spherical clusters but may struggle with clusters of more complex shapes.
We walked through how to implement the k-Means algorithm in Python, using it to identify spherical clusters within synthetic data. Moreover, we explored different methods to evaluate and visualize a clustering model’s performance, providing you with valuable tools to effectively analyze and group your data.
Whether it’s anomaly detection in time-series data or customer segmentation, k-Means can be a powerful tool in your data science arsenal. If you’re interested in anomaly detection, feel free to explore my recent article on the subject, written with Python enthusiasts in mind. Armed with this knowledge, you’re ready to embark on your own data exploration journey using k-Means clustering.
If you are interested in this topic, check out my recent article on anomaly detection with Python. And if you have any questions, please ask them in the comments.
Did you know that customer segmentation is an area where real-world data can be prone to bias and unfairness? If you’re concerned that your models may reflect the same bias, check out our latest article on addressing fairness in machine learning with fairlearn.
Sources and Further Reading
Books on Clustering
- “Data Clustering: Algorithms and Applications” by Charu C. Aggarwal: This book covers a wide range of clustering algorithms, including hierarchical clustering, and discusses their applications in various fields.
- “Data Mining: Practical Machine Learning Tools and Techniques” by Ian H. Witten and Eibe Frank: This book is a comprehensive introduction to data mining and machine learning, including a chapter on hierarchical clustering.
The links above to Amazon are affiliate links. By buying through these links, you support the Relataly.com blog and help to cover the hosting costs. Using the links does not affect the price.
Related Articles on Clustering
- Hierarchical clustering for customer segmentation in Python: We present an alternative approach to k-means that can determine the number of the clusters themselves and works well if the distributions of the groups in the data is more complex.
- Clustering crypto markets using affinity propagation in Python: This article applies cluster analysis to crypto markets and creates a market map for various cryptocurrencies.

