Financial analysts have long been fascinated by the prospect of predicting the prices of financial assets. In recent years, there has been increasing interest in using machine learning and deep learning techniques to generate predictions, in addition to traditional methods such as technical and fundamental analysis. Python libraries like Keras and Scikit-Learn make it relatively straightforward for those with programming experience to build a neural network for stock market forecasting. This tutorial will guide you through the process of creating a univariate model using a Keras neural network with LSTM layers to forecast the S&P500 index. By the end of this tutorial, you will have a model that can make single-step predictions for the stock market.
The rest of this article proceeds in two parts: We briefly introduce univariate modeling and neural networks. Then we start with the coding part and go through all the steps to train a neural network, including data ingestion, data preprocessing, and the design, training, testing, and usage of a predictive neural network model.
Disclaimer
This article does not constitute financial advice. Stock markets can be very volatile and are generally difficult to predict. Predictive models and other forms of analytics applied in this article only serve the purpose of illustrating machine learning use cases.
Single-Step Univariate Stock Market Prediction
The prediction approach described in this article is known as single-step single-variate time series forecasting. This approach is similar to technical chart analysis in that it assumes that predicting the price of an asset is fundamentally a time series problem. The goal is to identify patterns in a time series that indicate how the series will develop in the future.
This tutorial predicts the value for a single time step (1 day). In other words, we consider a single time series of data (single-variate). However, predicting multiple steps or increasing the time-step length would also be possible. In both cases, the predictions will range further into the future. I have covered this topic in a separate post on time series forecasting.
We will develop a univariate prediction model that predicts a single feature on historical prices for a specific period. More complex multivariate models use additional features such as moving averages, momentum indicators, or market sentiment. I have covered multivariate stock market prediction in a separate tutorial.
What are Recurrent Neural Networks?
Recurrent Neural Networks (RNNs) are particularly powerful for analyzing time series data because they use LSTM layers that allow information to flow back and forth through the network. This allows the RNN to learn patterns that may occur over long periods of time and potentially overlap, leading to more accurate predictions. RNNs differ from traditional feed-forward neural networks in that all information does not flow in a single direction from left to right. Instead, the output of the RNN is fed back into the network, allowing it to take into account past information when making predictions.
One of the primary advantages of RNNs is their ability to process sequential data, such as time series or natural language text. This is because the LSTM layers in an RNN allow the network to maintain a sense of memory and context, allowing it to understand the relationships between data points better and make more accurate predictions.
RNNs are commonly used in a wide range of applications, including language translation, speech recognition, and sentiment analysis. In these applications, the input data is often a sequence of words or other elements. The RNN can use its memory and context-aware processing to understand the meaning and relationships between the elements in the sequence.
Also: Stock Market Forecasting Neural Networks for Multi-Output Regression in Python
Creating a Univariate Forecasting Model using Keras Recurrent Neural Networks in Python
In this article, we will showcase the process of building a univariate forecast for the closing price of the S&P500 stock market index. To achieve this, we will use a Recurrent Neural Network (RNN) architecture with Long Short-Term Memory (LSTM) layers based on the popular Tensorflow library. In addition, we will employ various Python packages for data manipulation and analytics. The process of training and using the univariate model involves several key steps:
- Loading the data
- Exploring the data to identify trends and patterns
- Scaling and splitting the data to prepare it for modeling
- Creating the input shape to feed the data into the LSTM network
- Training the model on the training data set
- Forecasting future values using the trained model
- Visualizing and interpreting the forecasted results
By following these steps, we will be able to create a robust forecast for the closing price of the S&P500 stock market index.
The Python code is available in the relataly GitHub repository.
Please note that you will need some programming experience and familiarity with Python to follow along with this article. Understanding Neural Networks in all depth is not a prerequisite for this tutorial. But if you want to learn more about their architecture and functioning, I can recommend this YouTube video.
Prerequisites
Before starting the coding part, make sure that you have set up your Python 3 environment and required packages. If you don’t have an environment yet, you can follow the steps in this article to set up the Anaconda environment. Also, make sure you install all required packages. In this tutorial, we will be working with the following standard packages:
In addition, we will be using Keras (2.0 or higher) with Tensorflow backend and the machine learning library scikit-learn.
You can install packages using console commands:
- pip install <package name>
- conda install <package name> (if you are using the anaconda packet manager)
Step #1 Load the Data
Let’s start by setting up the imports and loading the price data from yahoo.finance.com via an API. To extract the data, we’ll use the pandas DataReader package – a popular library that provides a function to extract data from various Internet sources into pandas DataFrames. Note that if pandas DataReader does not work, you can use the yfinance package.
The following code extracts the price data for the S&P500 index from yahoo finance. If you wonder what “^GSPC” means, this is the symbol for the S&P500, a stock market index of the 500 most extensive stocks listed in the US stock market. You can use the symbols of other assets, e.g., BTC-USD for Bitcoin. The data is limited to the timeframe between 2010-01-01 and the current date. So when you execute the code, the results will show a more significant period, as in this tutorial.
# A tutorial for this file is available at www.relataly.com
# Tested with Python 3.88
import math
import numpy as np # Fundamental package for scientific computing with Python
import pandas as pd # For analysing and manipulating data
from datetime import date, timedelta # Date Functions
import matplotlib.pyplot as plt # For visualization
import matplotlib.dates as mdates # Formatting dates
from sklearn.metrics import mean_absolute_error, mean_squared_error # For measuring model performance / errors
from sklearn.preprocessing import MinMaxScaler #to normalize the price data
from tensorflow.keras.models import Sequential # Deep learning library, used for neural networks
from tensorflow.keras.layers import LSTM, Dense # Deep learning classes for recurrent and regular densely-connected layers
import tensorflow as tf
import seaborn as sns
sns.set_style('white', { 'axes.spines.right': False, 'axes.spines.top': False})
# check the tensorflow version and the number of available GPUs
print('Tensorflow Version: ' + tf.__version__)
physical_devices = tf.config.list_physical_devices('GPU')
print("Num GPUs:", len(physical_devices))
# Setting the timeframe for the data extraction
today = date.today()
end_date = today.strftime("%Y-%m-%d")
start_date = '2010-01-01'
# Getting S&P500 quotes
stockname = 'S&P500'
symbol = '^GSPC'
# You can either use webreader or yfinance to load the data from yahoo finance
# import pandas_datareader as webreader
# df = webreader.DataReader(symbol, start=start_date, end=end_date, data_source="yahoo")
import yfinance as yf #Alternative package if webreader does not work: pip install yfinance
df = yf.download(symbol, start=start_date, end=end_date)
# Taking a look at the shape of the dataset
print(df.shape)
df.head(5)Tensorflow Version: 2.6.0 Num GPUs: 1 [*********************100%***********************] 1 of 1 completed (3193, 6) Open High Low Close Adj Close Volume Date 2009-12-31 1126.599976 1127.640015 1114.810059 1115.099976 1115.099976 2076990000 2010-01-04 1116.560059 1133.869995 1116.560059 1132.989990 1132.989990 3991400000 2010-01-05 1132.660034 1136.630005 1129.660034 1136.520020 1136.520020 2491020000 2010-01-06 1135.709961 1139.189941 1133.949951 1137.140015 1137.140015 4972660000 2010-01-07 1136.270020 1142.459961 1131.319946 1141.689941 1141.689941 5270680000
Step #2 Explore the Data
When you load a new data set into your project, it is often a good idea to familiarize yourself with it before taking further steps. When working with time-series data, visually viewing the data in a line plot is the primary way. Use the following code to create the line plot for the S&P500 data.
# Creating a Lineplot
years = mdates.YearLocator()
fig, ax1 = plt.subplots(figsize=(16, 6))
ax1.xaxis.set_major_locator(years)
ax1.legend([stockname], fontsize=12)
plt.title(stockname + ' from '+ start_date + ' to ' + end_date)
sns.lineplot(data=df['Close'], label=stockname, linewidth=1.0)
plt.ylabel('S&P500 Points')
plt.show()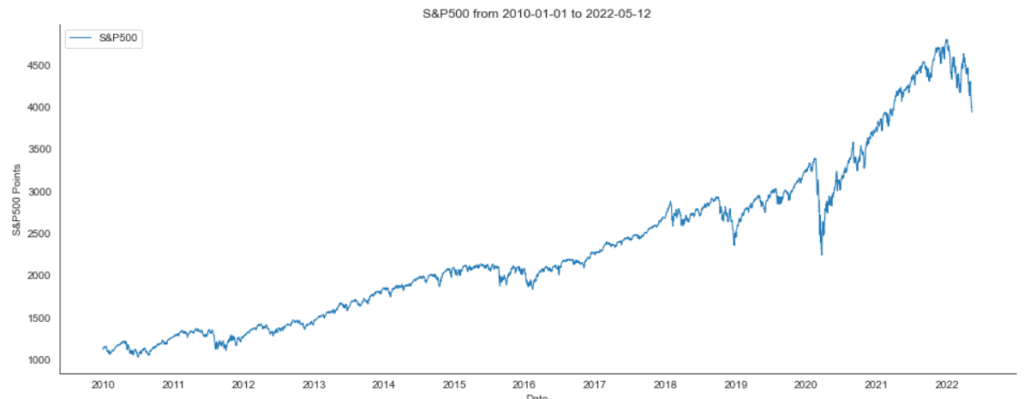
If you follow the course of the S&P500 stock markets a little, the chart above might look familiar to you.
Step #3 Scaling the Data
It’s best to scale the data before training a neural network. We will use the MinMaxScaler to normalize the price values in our data to a range between 0 and 1.
# Feature Selection - Only Close Data train_df = df.filter(['Close']) data_unscaled = train_df.values # Get the number of rows to train the model on 80% of the data train_data_length = math.ceil(len(data_unscaled) * 0.8) # Transform features by scaling each feature to a range between 0 and 1 mmscaler = MinMaxScaler(feature_range=(0, 1)) np_data = mmscaler.fit_transform(data_unscaled)
Step #4 Creating the Input Shape
Before we can begin with the training of the NN, we need to split the data into separate test sets for training and validation and ensure that it is in the right shape. We will train the NN on a decade of market price data. Then we predict the price of the next day based on the last 50 days of market prices. As illustrated below, we will use 80% of the data as training data and keep 20% as test data to later evaluate the performance of our univariate model.

Our neural network will have two layers, an input layer, and an output layer. The input data shape must correspond with the number of neurons in the neural network’s input layer. Therefore, we must also decide on the neural network architecture before bringing our data in the right shape.
4.1 Designing the Input Shape
Next, we create the training data based on which we will train our neural network. We make multiple slices of the training data (x_train), so-called mini-batches. The neural network processes the mini-batch one by one during the training process and creates a separate forecast for each mini-batch. The illustration below shows the shape of the data:
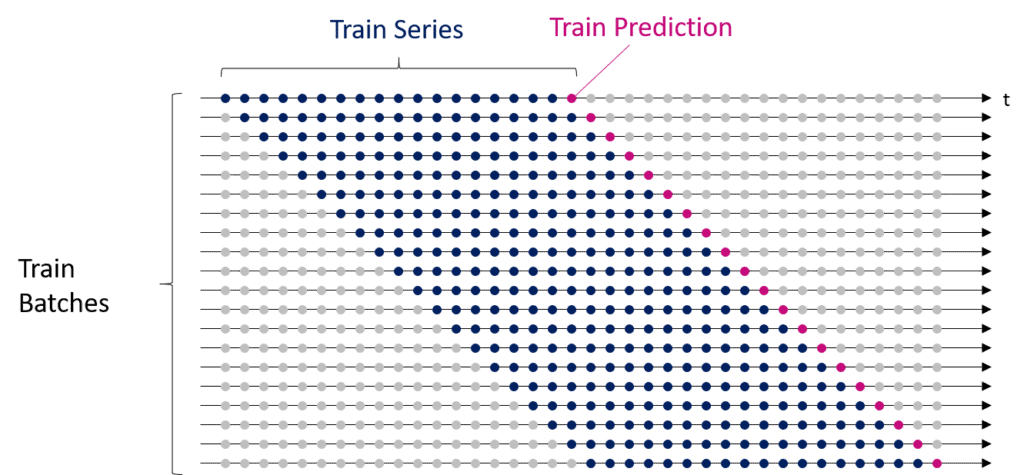
Neural networks learn in an iterative process. The algorithm reduces the prediction errors by adjusting the connection strength between the neurons (weights) in this process. The model needs a second list (y_train) to evaluate the forecast quality, containing the valid price values from our ground truth. The model compares the predictions with the ground truth during training and calculates the training error to minimize it over time.
4.2 Data Preprocessing
The code block below will carry out the steps to prepare the data. It is a standard procedure that will split the data into several mini-batches. Each minibatch contains an input sequence and a corresponding output sequence, the target.
# Set the sequence length - this is the timeframe used to make a single prediction
sequence_length = 50
# Prediction Index
index_Close = train_df.columns.get_loc("Close")
print(index_Close)
# Split the training data into train and train data sets
# As a first step, we get the number of rows to train the model on 80% of the data
train_data_len = math.ceil(np_data.shape[0] * 0.8)
# Create the training and test data
train_data = np_data[0:train_data_len, :]
test_data = np_data[train_data_len - sequence_length:, :]
# The RNN needs data with the format of [samples, time steps, features]
# Here, we create N samples, sequence_length time steps per sample, and 6 features
def partition_dataset(sequence_length, train_df):
x, y = [], []
data_len = train_df.shape[0]
for i in range(sequence_length, data_len):
x.append(train_df[i-sequence_length:i,:]) #contains sequence_length values 0-sequence_length * columsn
y.append(train_df[i, index_Close]) #contains the prediction values for validation (3rd column = Close), for single-step prediction
# Convert the x and y to numpy arrays
x = np.array(x)
y = np.array(y)
return x, y
# Generate training data and test data
x_train, y_train = partition_dataset(sequence_length, train_data)
x_test, y_test = partition_dataset(sequence_length, test_data)
# Print the shapes: the result is: (rows, training_sequence, features) (prediction value, )
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
# Validate that the prediction value and the input match up
# The last close price of the second input sample should equal the first prediction value
print(x_test[1][sequence_length-1][index_Close])
print(y_test[0])(1966, 50, 1) (1966,)
x_train contains 1966 mini-batches. Each contains a series of quotes for 50 dates. In y_train, we have 1966 validation values – one for each mini-batch. Be aware that numbers depend on the timeframe and vary when executing the code.
Step #5 Designing the Model Architecture
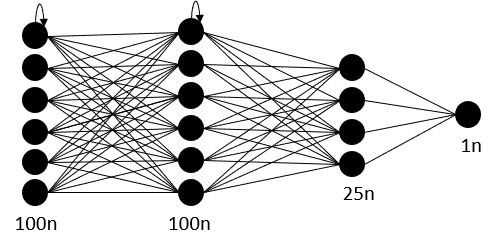
Before we can train the model, we first need to decide on the model’s architecture. Above all, the architecture comprises the type and number of layers and the number of neurons in each layer.
5.1 Choosing Layers
Determining the optimal number of layers for a neural network can be challenging and often requires trial and error. One approach is to try out different architectures and see which one performs best. In this case, we will use a fully connected network with four layers, consisting of two layers of the LSTM class and two layers of the Dense class from the Keras library. This architecture was chosen because it is relatively simple and a good starting point for addressing time series problems. The architecture and performance of the univariate model can then be tested and refined through multiple iterations.
5.2 Choosing the Number of Neurons
When selecting the number of neurons for a neural network layer, there are a few general guidelines to follow:
- A larger number of neurons can allow the model to capture more complex patterns in the data, but it may also increase the risk of overfitting.
- A smaller number of neurons can reduce the risk of overfitting, but it may also limit the model’s ability to capture complex patterns.
- It is generally recommended to start with a smaller number of neurons and increase the number if necessary.
One approach to determining the number of neurons is to use the “rule of thumb” method, which suggests using the following formula: (number of input neurons + number of output neurons) * 2/3. However, the optimal number of neurons will depend on the specific problem being solved and the characteristics of the data.
For our specific example, the input data consists of values for 50 dates, so the input layer should have at least 50 neurons for each value. The second layer should have 35 neurons according to the formula ((50 + 1) * 2 / 3), and the last layer should have only one neuron, as the prediction will contain a single price point for a single time step.
# Configure the neural network model model = Sequential() neurons = sequence_length # Model with sequence_length Neurons # inputshape = sequence_length Timestamps model.add(LSTM(neurons, return_sequences=True, input_shape=(x_train.shape[1], 1))) model.add(LSTM(neurons, return_sequences=False)) model.add(Dense(35, activation='relu')) model.add(Dense(1)) # Compile the model model.compile(optimizer='adam', loss='mean_squared_error')
Step #6 Train the Univariate Model
Now that we have prepared our data and defined our model, it’s time to fit the model to the data and start training. Training a machine learning model involves adjusting the model’s parameters to minimize the error between the predicted and actual values. This process can take a varying amount of time, depending on the complexity of the model and the size of the dataset. For instance, the training time is usually a couple of minutes on my local notebook processor (Intel Core i7).
# Training the model model.fit(x_train, y_train, batch_size=16, epochs=25)
Epoch 1/25 157/157 [==============================] - 8s 10ms/step - loss: 0.0025 Epoch 2/25 157/157 [==============================] - 1s 9ms/step - loss: 1.2553e-04 Epoch 3/25 157/157 [==============================] - 1s 9ms/step - loss: 1.2324e-04 Epoch 4/25 157/157 [==============================] - 1s 9ms/step - loss: 1.1924e-04 Epoch 5/25 157/157 [==============================] - 1s 9ms/step - loss: 1.1989e-04 Epoch 6/25 157/157 [==============================] - 1s 9ms/step - loss: 1.1564e-04 Epoch 7/25 157/157 [==============================] - 1s 9ms/step - loss: 1.0769e-04 Epoch 8/25 157/157 [==============================] - 1s 9ms/step - loss: 1.0273e-04 Epoch 9/25 157/157 [==============================] - 1s 9ms/step - loss: 9.0550e-05 Epoch 10/25 157/157 [==============================] - 1s 9ms/step - loss: 9.1702e-05 Epoch 11/25 157/157 [==============================] - 1s 8ms/step - loss: 8.8220e-05 Epoch 12/25 157/157 [==============================] - 1s 9ms/step - loss: 1.0555e-04 Epoch 13/25 ... Epoch 24/25 157/157 [==============================] - 1s 9ms/step - loss: 6.1625e-05 Epoch 25/25 157/157 [==============================] - 1s 9ms/step - loss: 4.8550e-05 <tensorflow.python.keras.callbacks.History at 0x244a926acd0>
We have fitted our model to the training data.
Step #7 Creating the Univariate Stock Market Forecasting
So how does our stock market prediction model perform? We need to feed the model with the test data to evaluate the model’s performance. For this purpose, we provide the test data (x_test) that we have generated in a previous step to the model to get some predictions. We must remember that we initially scaled the input data to 0 and 1. Therefore, before interpreting the results, we must inverse the MinMaxScaling from the predictions.
# Get the predicted values y_pred_scaled = model.predict(x_test) y_pred = mmscaler.inverse_transform(y_pred_scaled) y_test_unscaled = mmscaler.inverse_transform(y_test.reshape(-1, 1))
Step #8 Evaluate Model Performance
Different indicators can help us to evaluate the performance of our model. We calculate the forecast error by subtracting valid test data (y_test) from predictions.
# Mean Absolute Error (MAE)
MAE = mean_absolute_error(y_test_unscaled, y_pred)
print(f'Median Absolute Error (MAE): {np.round(MAE, 2)}')
# Mean Absolute Percentage Error (MAPE)
MAPE = np.mean((np.abs(np.subtract(y_test_unscaled, y_pred)/ y_test_unscaled))) * 100
print(f'Mean Absolute Percentage Error (MAPE): {np.round(MAPE, 2)} %')
# Median Absolute Percentage Error (MDAPE)
MDAPE = np.median((np.abs(np.subtract(y_test_unscaled, y_pred)/ y_test_unscaled)) ) * 100
print(f'Median Absolute Percentage Error (MDAPE): {np.round(MDAPE, 2)} %')MAE: 32.0 RMSE: 17.6
The MAE can be negative or positive. If it is positive, our predictions lie below the valid values. For our model, the calculated MAE is (32.0). From the MAE, we can tell that our model generally tends to predict a bit too pessimistically.
The mean squared error (RMSE) is always positive. More significant errors tend to impact the RMSE as they are squared substantially. In our case, the RMSE is 17.6, indicating that the prediction error is relatively constant. In other words, the predictions are mostly not entirely wrong.
Visualizing test predictions helps in the process of evaluating the model. Therefore we will plot predicted and valid values.
# The date from which on the date is displayed
display_start_date = "2019-01-01"
# Add the difference between the valid and predicted prices
train = pd.DataFrame(train_df[:train_data_length + 1]).rename(columns={'Close': 'y_train'})
valid = pd.DataFrame(train_df[train_data_length:]).rename(columns={'Close': 'y_test'})
valid.insert(1, "y_pred", y_pred, True)
valid.insert(1, "residuals", valid["y_pred"] - valid["y_test"], True)
df_union = pd.concat([train, valid])
# Zoom in to a closer timeframe
df_union_zoom = df_union[df_union.index > display_start_date]
# Create the lineplot
fig, ax1 = plt.subplots(figsize=(16, 8), sharex=True)
plt.title("Predictions vs Ground Truth")
sns.set_palette(["#090364", "#1960EF", "#EF5919"])
plt.ylabel(stockname, fontsize=18)
sns.lineplot(data=df_union_zoom[['y_train', 'y_pred', 'y_test']], linewidth=1.0, dashes=False, ax=ax1)
# Create the barplot for the absolute errors
df_sub = ["#2BC97A" if x > 0 else "#C92B2B" for x in df_union_zoom["residuals"].dropna()]
ax1.bar(height=df_union_zoom['residuals'].dropna(), x=df_union_zoom['residuals'].dropna().index, width=3, label='absolute errors', color=df_sub)
plt.legend()
plt.show()We can see that the orange zone contains the test predictions. The grey area marks the difference between test predictions and ground truth. As indicated by the different performance measures, we can see that the predictions are typically near the ground truth.
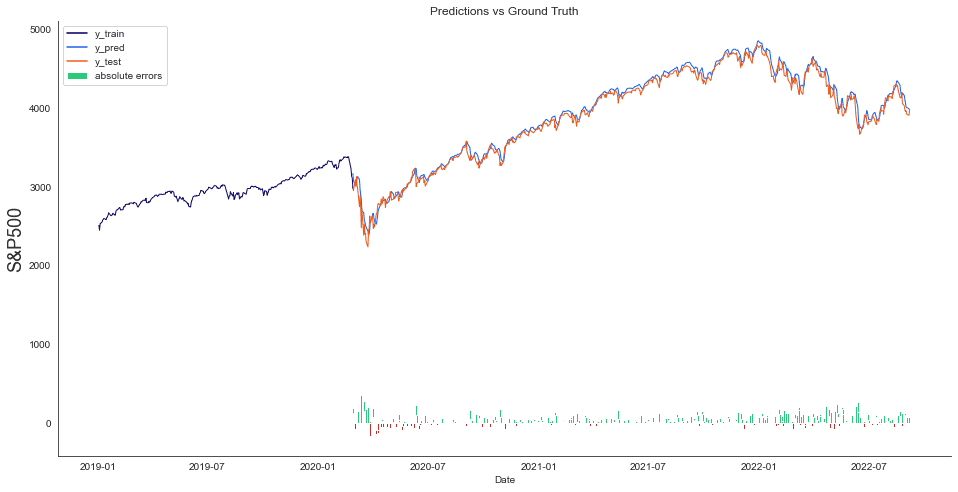
We have also added the absolute errors on the bottom. Where the difference is negative, the predicted value was too optimistic. Where the difference is positive, the predictive value was too pessimistic.
Step #9 Stock Market Prediction – Predicting a Single Day Ahead
Now that we have tested our model, we can use it to make a prediction. We use a new data set as the input for our prediction model. The model returns a forecast for a single time the next day.
# Get fresh data
df_new = df.filter(['Close'])
# Get the last N day closing price values and scale the data to be values between 0 and 1
last_days_scaled = mmscaler.transform(df_new[-sequence_length:].values)
# Create an empty list and Append past n days
X_test = []
X_test.append(last_days_scaled)
# Convert the X_test data set to a numpy array and reshape the data
X_test = np.array(X_test)
X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1], 1))
# Get the predicted scaled price, undo the scaling and output the predictions
pred_price = model.predict(X_test)
pred_price_unscaled = mmscaler.inverse_transform(pred_price)
# Print last price and predicted price for the next day
price_today = round(df_new['Close'][-1], 2)
predicted_price = round(pred_price_unscaled.ravel()[0], 2)
percent_change = round((predicted_price * 100)/price_today - 100, 2)
prefix = '+' if percent_change > 0 else ''
print(f'The close price for {stockname} at {today} was {price_today}')
print(f'The predicted close price for the next day is {predicted_price} ({prefix}{percent_change}%)')The price for S&P500 on 2020-04-04 was: 2578.0
The predicted S&P500 price on the date 2020-04-05 is: 2600.0
So, the model predicts a value of 2600.0 for the S&P500 on 2020-04-07.
Summary
In this tutorial, you have learned to create, train and test a four-layered recurrent neural network for stock market prediction using Python and Keras. Finally, we have used this model to predict the S&P500 stock market index. You can easily create models for other assets by replacing the stock symbol with another stock code. A list of common symbols for stocks or stock indexes is available on yahoo.finance.com. Don’t forget to retrain the model with a fresh copy of the price data.
The model created in this post makes predictions for a single time step. If you want to learn how to make time-series predictions that range further, you might want to check out the part II of this tutorial series: Creating a Multistep Forecast in Python.
I hope you enjoyed this article. I am always trying to improve and learn from my audience. So, please let me know in the comments if you have questions or remarks!
Sources and Further Reading
- Charu C. Aggarwal (2018) Neural Networks and Deep Learning
- Jansen (2020) Machine Learning for Algorithmic Trading: Predictive models to extract signals from market and alternative data for systematic trading strategies with Python
- Aurélien Géron (2019) Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems
- David Forsyth (2019) Applied Machine Learning Springer
- Andriy Burkov (2020) Machine Learning Engineering
- ChatGPT helped to revise this article.
- Images created with Midjourney.
The links above to Amazon are affiliate links. By buying through these links, you support the Relataly.com blog and help to cover the hosting costs. Using the links does not affect the price.
If you want to learn about an alternative approach to univariate stock market forecasting, consider this article on Facebook Prophet.
This was a great article! The writing was clear and the code was easy to follow and use in my own project. This has helped me extend my forecasting functionality greatly!
Thanks a ton Florian!
This is a great article with a ton of useful Python techniques for plotting stock data. The prediction routines are very good. Thank you for sharing!
8.4. Closing Price: 2,749.98 – aaaaalmost. 🙂