Time series analysis and forecasting is a tough nut to crack, but the ARIMA model has been cracking it for decades. ARIMA, short for “Auto-Regressive Integrated Moving Average,” is a powerful statistical modeling technique for time series analysis. It’s particularly effective when the time series you’re analyzing follows a clear pattern, like seasonal changes in weather or sales. ARIMA has been used to forecast everything from beer sales to order quantities, and this tutorial will show you how to build your own ARIMA model in Python. You’ll be making predictions like a pro in no time!
This tutorial proceeds in two parts: The first part covers the concepts behind ARIMA. You will learn how ARIMA works, what Stationarity means, and when it is appropriate to use ARIMA. The second part is a Python hands-on tutorial that applies auto-ARIMA to the Sales Forecasting domain. We’ll be working with a time series of beer sales, and our goal is to predict how the beer sales quantities will evolve in the coming years. First, we check if the time series is stationary. Then we train an ARIMA forecasting model. Finally, we use the model to produce a sales forecast and measure the model’s performance.
About Sales Forecasting
Sales forecasting is a crucial business strategy that involves predicting future sales volumes for a product (for example, beer) or service. It leverages sophisticated statistical and analytical techniques, such as time series analysis or machine learning algorithms, to scrutinize historical sales data. By identifying trends and patterns within this data, businesses can make informed predictions about their future sales performance.
This strategic forecasting plays a pivotal role in business operations. It is instrumental in guiding key decisions surrounding production, inventory management, staffing, and various other operational elements. By honing in on accurate sales forecasting, businesses can strike the perfect balance – maintaining enough inventory to meet customer demand without overproducing or overstocking. This equilibrium ensures a smooth flow in the supply chain and avoids unnecessary costs tied to excess production or storage.
Furthermore, sales forecasting serves as a roadmap for business growth. It aids in identifying potential market opportunities and predicting future sales revenue. This valuable foresight enables businesses to strategically plan their expansion, ensuring resources are optimally utilized and future goals are met. With this in-depth understanding of sales forecasting, businesses can stay ahead of market trends, navigate through business challenges, and ultimately steer towards success.

Introduction to ARIMA Time Series Modelling
ARIMA models provide an alternative approach to time series forecasting that differs significantly from machine learning methods. Working with ARIMA requires a good understanding of Stationarity and knowledge of the transformations used to make time-series data stationary. The concept of Stationarity is, therefore, first on our schedule.
The Concept of Stationarity
Stationarity is an essential concept in stochastic processes that describes the nature of a time series. We consider a time series strictly stationary if its statistical properties do not change over time. In this case, summary statistics, such as the mean and variance, do not change over time. However, the time-series data we encounter in the real world often show a trend or significant irregular fluctuations, making them non-stationary or weakly stationary.
So why is Stationarity such an essential concept for ARIMA? If a time series is stationary, we can assume that the past values of the time series are predictive of future development. In other words, a stationary time series exhibits consistent behavior that makes it predictable. On the other hand, a non-stationary time series is characterized by a kind of random behavior that will be difficult to capture in modeling. Namely, if random movements characterized the past, there is a high probability that the future will be no different.
Fortunately, in many cases, it is possible to transform a time series that is non-stationary into a stationary form and, in this way, build better prediction models.
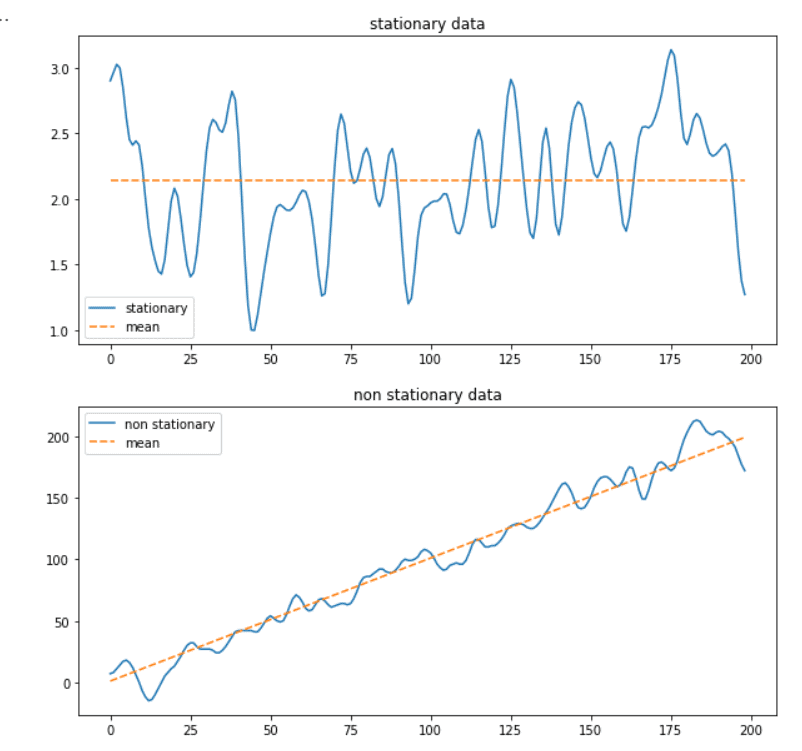
How to Test Whether a Time Series is Stationary
The first step in the ARIMA modeling approach is determining whether a time series is stationary. There are different ways to determine whether a time series is stationary:
- Plotting: We can plot the time series and visually check if it shows consistent behavior or changes over a more extended period.
- Summary statistics: We can split the time series into different periods and calculate the summary statistics, such as the variance. If these metrics are subject to significant changes, the time series is non-stationary. However, the results will also depend on the respective periods, leading to false conclusions.
- Statistic tests: There are various tests to determine the stationary of a time series, such as Kwiatkowski–Phillips–Schmidt–Shin, Augmented Dickey-Fuller, or Phillips–Perron. These tests systematically check a time series and measure the results against the null hypothesis, providing an indicator of the trustworthiness of the results.
What is an (S)ARIMA Model?
As the name implies, ARIMA uses autoregression (AR), integration (differencing), and moving averages (MA) to fit a linear regression model to a time series.
ARIMA Parameters
The default notation for ARIMA is a model with parameters p, d, and q, whereby each parameter takes an integer value:
- d (differencing): In the case of a non-stationary time series, there is a chance to remove a trend from the data by differencing once or several times, thus bringing the data to a stationary state. The model parameter d determines the order of the differentiation. A value of d = 0 simplifies the ARIMA model to an ARMA model, lacking the integration aspect. If this is the case, we do not need to integrate the function because the time series is already stationary.
- p (order of the AR terms): The autoregressive process describes the dependent relationship between an observation and several lagged observations (lags). Predictions are then based on past data from the same time series using linear functions. p = 1 means the model uses values that lag by one period.
- q (order of the MA terms): The parameter q determines the number of lagged forecast errors in the prediction equation. In contrast to the AR process, the MA process assumes that values at a future point in time depend on the errors made by predictions at current and past points in time. This means that it is not previous events that determine the predictions but rather the previous estimation or prediction errors used to calculate the following time series value.
SARIMA
In the real world, many time series have seasonal effects. Examples are monthly retail sales figures, temperature reports, weekly airline passenger data, etc. To consider this, we can specify a seasonal range (e.g., m=12 for monthly data) and additional seasonal AR or MA components for our model that deal with seasonality. Such a model is also called a SARIMA model, and we can define it as a model(p, d, q)(P, D, Q)[m].
Auto-(S)ARIMA
When working with ARIMA, we can set the model parameters manually or use auto-ARIMA and let the model search for the optimal parameters. We do this by varying the parameters and then testing against Stationarity. With the seasonal option enabled, the process tries to identify the optimal hyperparameters for the seasonal components of the model. Auto-ARIMA works by conducting differencing tests to determine the order of differencing, d and then fitting models with parameters in defined ranges, e.g., start_p, max_p as well as start_q, max_q. If our model has a seasonal component, we can also define parameter ranges for the seasonal part of the model.
Creating a Sales Forecast with ARIMA in Python
Having grasped the fundamental concepts behind ARIMA (AutoRegressive Integrated Moving Average), we’re now ready to dive into the practical aspect of crafting a sales forecasting model in Python. Utilizing ARIMA for forecasting sales data is an esteemed practice owing to the algorithm’s adeptness in modeling seasonal changes combined with long-term trends – a characteristic commonly exhibited by sales data.
In this tutorial, we’ll be employing a dataset representing the monthly beer sales across the United States from 1992 through 2018, recorded in millions of US dollars. Our objective is to construct a robust time series model using ARIMA to accurately predict future sales trends.
When it comes to the technological aspect, we’ll be using the Python-based ‘statsmodels’ and ‘pmdarima’ libraries to build our ARIMA sales forecasting model. So, if you’re ready to harness the power of Python and ARIMA for sales prediction, let’s get started!
The code is available on the GitHub repository.

Prerequisites
Before we start coding, ensure you have set up your Python 3 environment and required packages. If you don’t have an environment, you can follow this tutorial to set up the Anaconda environment.
Also, make sure you install all required packages. In this tutorial, we will be working with the following standard packages:
In addition, we will be using the statsmodels library and pmdarima.
You can install packages using console commands:
- pip install <package name>
- conda install <package name> (if you are using the anaconda packet manager)
Step #1 Load the Sales Data to Our Python Project
In the initial step of this tutorial, we commence by setting up the necessary Python environment. We import several packages that we’ll be using for data manipulation, visualization, and implementing machine learning models. We then fetch the dataset we’ll be working with – the monthly beer sales in the United States from 1992 through 2018. This data is sourced from a publicly accessible URL and loaded into a pandas DataFrame.
# A tutorial for this file is available at www.relataly.com
# Tested with Python 3.88
# Setting up packages for data manipulation and machine learning
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import pmdarima as pm
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.seasonal import seasonal_decompose
import seaborn as sns
sns.set_style('white', { 'axes.spines.right': False, 'axes.spines.top': False})
# Link to the dataset:
# https://www.kaggle.com/bulentsiyah/for-simple-exercises-time-series-forecasting
path = "https://raw.githubusercontent.com/flo7up/relataly_data/main/alcohol_sales/BeerWineLiquor.csv"
df = pd.read_csv(path)
df.head()date beer 0 1/1/1992 1509 1 2/1/1992 1541 2 3/1/1992 1597 3 4/1/1992 1675 4 5/1/1992 1822
As shown above, the sales figures in this dataset stem from the first day of each month.
Step #2 Visualize the Time Series and Check it for Stationarity
Before modeling the sales data, we visualize the time series and test it for Stationarity. Visualization helps us choose the parameters for our ARIMA model, thus making it an essential step.
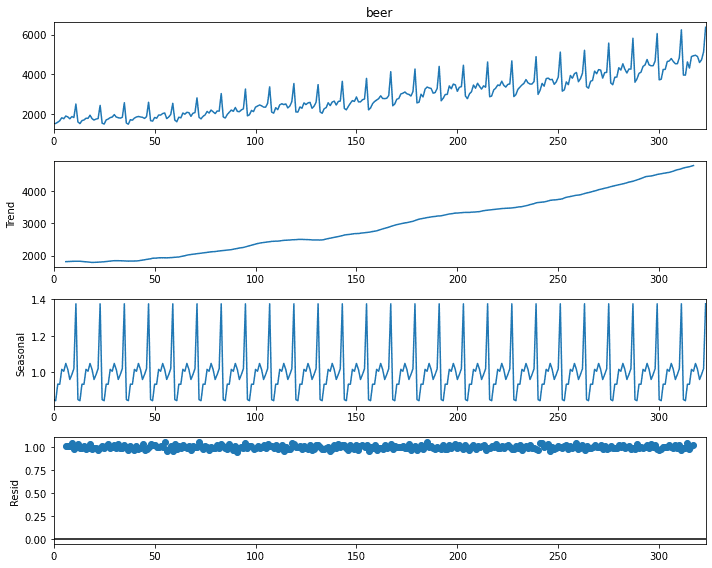
First, we will look at the different components of the time series. We do this by using the seasonal_decompose function of the statsmodels library.
# Decompose the time series plt.rcParams["figure.figsize"] = (10,6) result = seasonal_decompose(df['beer'], model='multiplicative', period = 12) result.plot() plt.show()
To test for Stationarity, we use the ADFuller test. It is common to run this test multiple times throughout a data science project. Therefore, we create a function that we can then reuse later.
def check_stationarity(df_sales, title_string, labels):
# Visualize the data
fig, ax = plt.subplots(figsize=(16, 8))
plt.title(title_string, fontsize=14)
if df_sales.index.size > 12:
df_sales['ma_12_month'] = df_sales['beer'].rolling(window=12).mean()
df_sales['ma_25_month'] = df_sales['beer'].rolling(window=25).mean()
sns.lineplot(data=df_sales[['beer', 'ma_25_month', 'ma_12_month']], palette=sns.color_palette("mako_r", 3))
plt.legend(title='Smoker', loc='upper left', labels=labels)
else:
sns.lineplot(data=df_sales[['beer']])
plt.show()
sales = df_sales['beer'].dropna()
# Perform an Ad Fuller Test
# the default alpha = .05 stands for a 95% confidence interval
adf_test = pm.arima.ADFTest(alpha = 0.05)
print(adf_test.should_diff(sales))
df_sales = pd.DataFrame(df['beer'], columns=['beer'])
df_sales.index = pd.to_datetime(df['date'])
title = "Beer sales in the US between 1992 and 2018 in million US$/month"
labels = ['beer', 'ma_12_month', 'ma_25_month']
check_stationarity(df_sales, title, labels)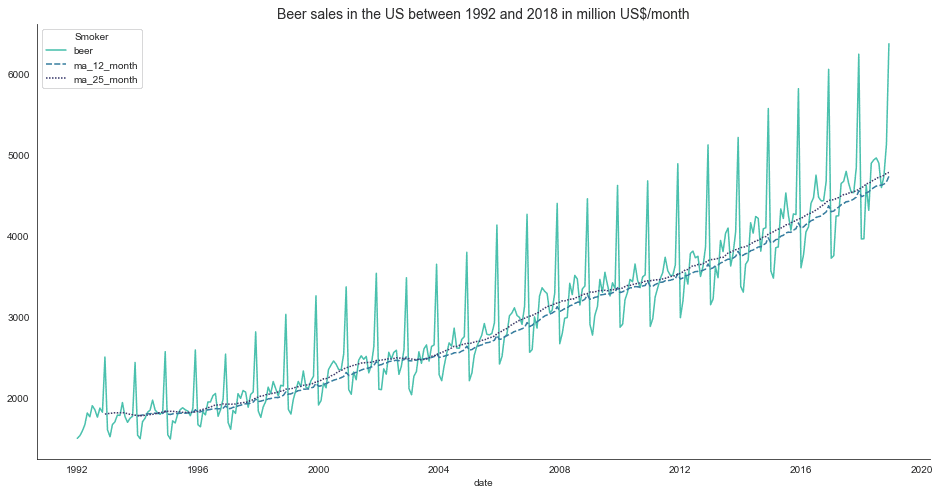
The data does not appear to be stationary. We can see that our time series is steadily increasing and shows annual seasonality. The steady increase indicates a continuous growth in beer consumption over the last decades. The seasonality in the sales data likely results from people drinking more beer in summer than in other seasons.
Step #3 Exemplary Differencing and Autocorrelation
The chart from the previous section shows that our time series is non-stationary. The reason is that it follows a clear upward trend. We also know that the time series has a seasonal component. Therefore, we need to define additional parameters and construct a SARIMA model.
Before we use auto-correlation to determine the optimal parameters, we will try manual differencing to make the time series stationary. There is no guarantee that differencing works. It is essential to remember that differencing can sometimes also worsen prediction performance. So be careful, not to overdifference! We could also trust that the auto-ARIMA model chooses the best parameters for us. However, we should always validate the selected parameters.
The ideal differencing parameter is the least number of differencing steps to achieve a stationary time series. We will monitor the results with autocorrelation plots to check whether differencing was successful.
We print the autocorrelation for the original time series and after the first and second-order differencing.
# 3.1 Non-seasonal part
def auto_correlation(df, prefix, lags):
plt.rcParams.update({'figure.figsize':(7,7), 'figure.dpi':120})
# Define the plot grid
fig, axes = plt.subplots(3,2, sharex=False)
# First Difference
axes[0, 0].plot(df)
axes[0, 0].set_title('Original' + prefix)
plot_acf(df, lags=lags, ax=axes[0, 1])
# First Difference
df_first_diff = df.diff().dropna()
axes[1, 0].plot(df_first_diff)
axes[1, 0].set_title('First Order Difference' + prefix)
plot_acf(df_first_diff, lags=lags - 1, ax=axes[1, 1])
# Second Difference
df_second_diff = df.diff().diff().dropna()
axes[2, 0].plot(df_second_diff)
axes[2, 0].set_title('Second Order Difference' + prefix)
plot_acf(df_second_diff, lags=lags - 2, ax=axes[2, 1])
plt.tight_layout()
plt.show()
auto_correlation(df_sales['beer'], '', 10)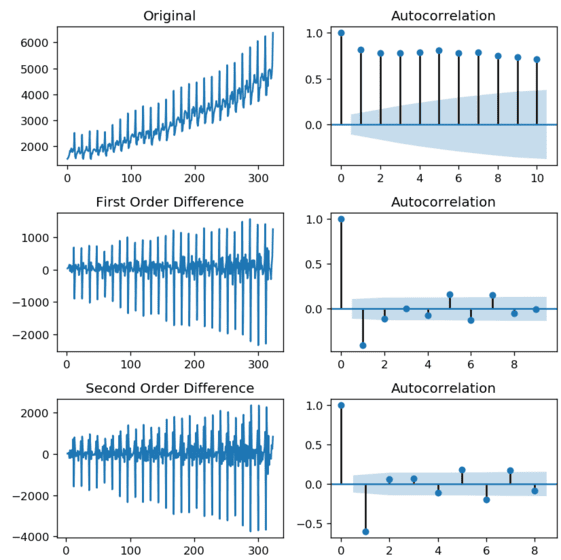
(0.019143247561160443, False)
The charts above show that the time series becomes stationary after one order differencing. However, we can see that the lag goes into the negative very quickly, which indicates overdifferencing.
Next, we perform the same procedure for the seasonal part of our time series.
# 3.2 Seasonal part # Reduce the timeframe to a single seasonal period df_sales_s = df_sales['beer'][0:12] # Autocorrelation for the seasonal part auto_correlation(df_sales_s, '', 10)
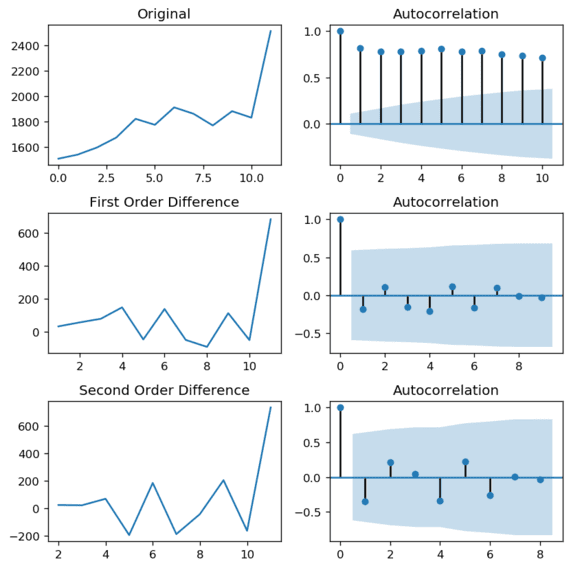
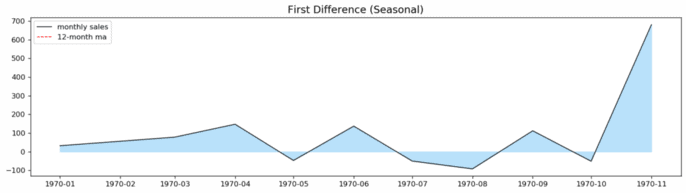
# Check if the first difference of the seasonal period is stationary df_diff = pd.DataFrame(df_sales_s.diff()) df_diff.index = pd.date_range(df_sales_s.diff().iloc[1], periods=12, freq='MS') check_stationarity(df_diff, "First Difference (Seasonal)", ['difference'])
(0.99, True)
After first order differencing, the seasonal part of the time series is stationary. The autocorrelation plot shows that the values go into the negative but remain within acceptable boundaries. Second-order differencing does not seem to improve these values. Consequently, we conclude that first-order differencing is a good choice for the D parameter.
Step #4 Finding an Optimal Model with Auto-ARIMA
Next, we auto-fit an ARIMA model to our time series. In this way, we ensure that we can later measure the performance of our model against a fresh set of data that the model has not seen so far. We will split our dataset into train and test in preparation for this.
Once we have created the train and test data sets, we can configure the parameters for the auto_arima stepwise optimization. By setting max_d = 1, we tell the model to test no-differencing and first-order differencing. Also, we set max_p and max_q to 3.
To deal with the seasonality in our time series, we set the “seasonal” parameter to True and the “m” parameter to 12 data points. We turn our model into a SARIMA model that allows us to configure additional D, P, and Q parameters. We define a max value for Q and P of 3. Previously we have already seen that further differencing does not improve the Stationarity. Therefore, we can set the value of D to 1.
After configuring the parameters, we next fit the model to the time series. The model will try to find the optimal parameters and choose the model with the least AIC.
# split into train and test
pred_periods = 30
split_number = df_sales['beer'].count() - pred_periods # corresponds to a prediction horizion of 2,5 years
df_train = pd.DataFrame(df_sales['beer'][:split_number]).rename(columns={'beer':'y_train'})
df_test = pd.DataFrame(df_sales['beer'][split_number:]).rename(columns={'beer':'y_test'})
# auto_arima
model_fit = pm.auto_arima(df_train, test='adf',
max_p=3, max_d=3, max_q=3,
seasonal=True, m=12,
max_P=3, max_D=2, max_Q=3,
trace=True,
error_action='ignore',
suppress_warnings=True,
stepwise=True)
# summarize the model characteristics
print(model_fit.summary())Performing stepwise search to minimize aic ARIMA(2,0,2)(1,1,1)[12] intercept : AIC=inf, Time=3.89 sec ARIMA(0,0,0)(0,1,0)[12] intercept : AIC=3383.210, Time=0.02 sec ARIMA(1,0,0)(1,1,0)[12] intercept : AIC=3351.655, Time=0.38 sec ARIMA(0,0,1)(0,1,1)[12] intercept : AIC=3364.350, Time=1.09 sec ARIMA(0,0,0)(0,1,0)[12] : AIC=3604.145, Time=0.02 sec ARIMA(1,0,0)(0,1,0)[12] intercept : AIC=3349.908, Time=0.11 sec ARIMA(1,0,0)(0,1,1)[12] intercept : AIC=3351.532, Time=0.29 sec ARIMA(1,0,0)(1,1,1)[12] intercept : AIC=3353.520, Time=1.24 sec ARIMA(2,0,0)(0,1,0)[12] intercept : AIC=3312.656, Time=0.10 sec ARIMA(2,0,0)(1,1,0)[12] intercept : AIC=3314.483, Time=0.57 sec ARIMA(2,0,0)(0,1,1)[12] intercept : AIC=3314.378, Time=0.30 sec ARIMA(2,0,0)(1,1,1)[12] intercept : AIC=3305.552, Time=3.02 sec ARIMA(2,0,0)(2,1,1)[12] intercept : AIC=3291.425, Time=4.19 sec ARIMA(2,0,0)(2,1,0)[12] intercept : AIC=3306.914, Time=3.06 sec ARIMA(2,0,0)(3,1,1)[12] intercept : AIC=3276.501, Time=4.67 sec ARIMA(2,0,0)(3,1,0)[12] intercept : AIC=3282.240, Time=5.24 sec ARIMA(2,0,0)(3,1,2)[12] intercept : AIC=inf, Time=7.39 sec ARIMA(2,0,0)(2,1,2)[12] intercept : AIC=inf, Time=4.74 sec ARIMA(1,0,0)(3,1,1)[12] intercept : AIC=3313.877, Time=5.17 sec ARIMA(3,0,0)(3,1,1)[12] intercept : AIC=3246.820, Time=5.72 sec ARIMA(3,0,0)(2,1,1)[12] intercept : AIC=3255.313, Time=5.33 sec ARIMA(3,0,0)(3,1,0)[12] intercept : AIC=3249.998, Time=6.77 sec ARIMA(3,0,0)(3,1,2)[12] intercept : AIC=inf, Time=8.39 sec ARIMA(3,0,0)(2,1,0)[12] intercept : AIC=3259.938, Time=3.55 sec ... =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step).
Auto-ARIMA has determined that the best model is (3,0,0)(3,1,1). These results match the results from section 3, in which we manually performed differencing.
Step #5 Simulate the Time Series using in-sample Forecasting
Now that we have trained our model, we want to use it to simulate the entire time series. We will do this by calling the predict method in the sample function. The prediction will match the same period as the original time series with which we trained the model. Because the model predicts one step, the prediction results will naturally be close to the actual values.
# Generate in-sample Predictions
# The parameter dynamic=False means that the model makes predictions upon the lagged values.
# This means that the model is trained until a point in the time-series and then tries to predict the next value.
pred = model_fit.predict_in_sample(dynamic=False) # works only with auto-arima
df_train['y_train_pred'] = pred
# Calculate the percentage difference
df_train['diff_percent'] = abs((df_train['x_train'] - pred) / df_train['x_train'])* 100
# Print the predicted time-series
fig, ax1 = plt.subplots(figsize=(16, 8))
plt.title("In Sample Sales Prediction", fontsize=14)
sns.lineplot(data=df_train[['x_train', 'y_train_pred']], linewidth=1.0)
# Print percentage prediction errors on a separate axis (ax2)
ax2 = ax1.twinx()
ax2.set_ylabel('Prediction Errors in %', color='purple', fontsize=14)
ax2.set_ylim([0, 50])
ax2.bar(height=df_train['diff_percent'][20:], x=df_train.index[20:], width=20, color='purple', label='absolute errors')
plt.legend()
plt.show()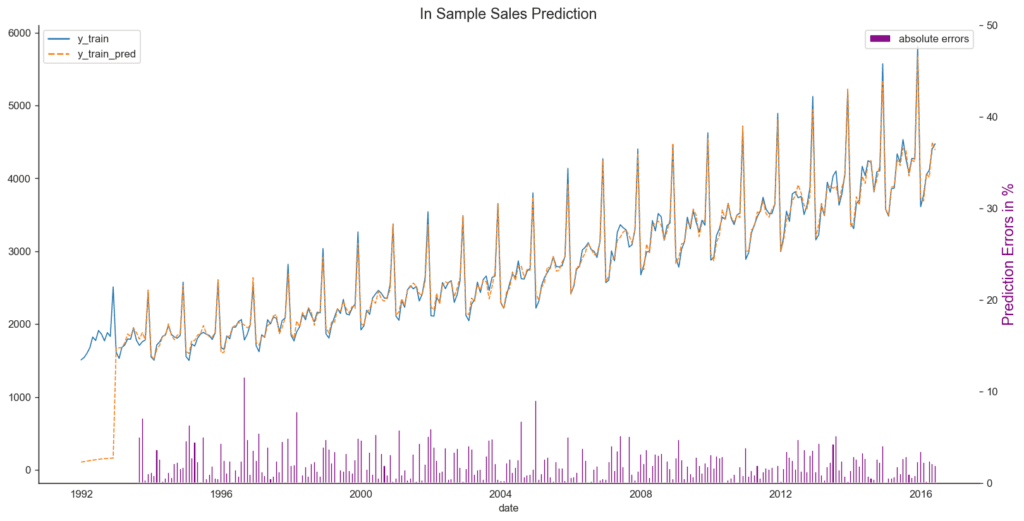
Next, we take a look at the prediction errors.
Step #6 Generate and Visualize a Sales Forecast
Now that we have trained an optimal model, we are ready to generate a sales forecast. First, we specify the number of periods that we want to predict. In addition, we create an index from the number of predictions adjacent to the original time series and continue it (prediction_index).
# Generate prediction for n periods,
# Predictions start from the last date of the training data
test_pred = model_fit.predict(n_periods=pred_periods, dynamic=False)
df_test['y_test_pred'] = test_pred
df_union = pd.concat([df_train, df_test])
df_union.rename(columns={'beer':'y_test'}, inplace=True)
# Print the predicted time-series
fig, ax = plt.subplots(figsize=(16, 8))
plt.title("Test/Pred Comparison", fontsize=14)
sns.despine();
sns.lineplot(data=df_union[['y_train', 'y_train_pred', 'y_test', 'y_test_pred']], linewidth=1.0, dashes=False, palette='muted')
ax.set_xlim([df_union.index[150],df_union.index.max()])
plt.legend()
plt.show()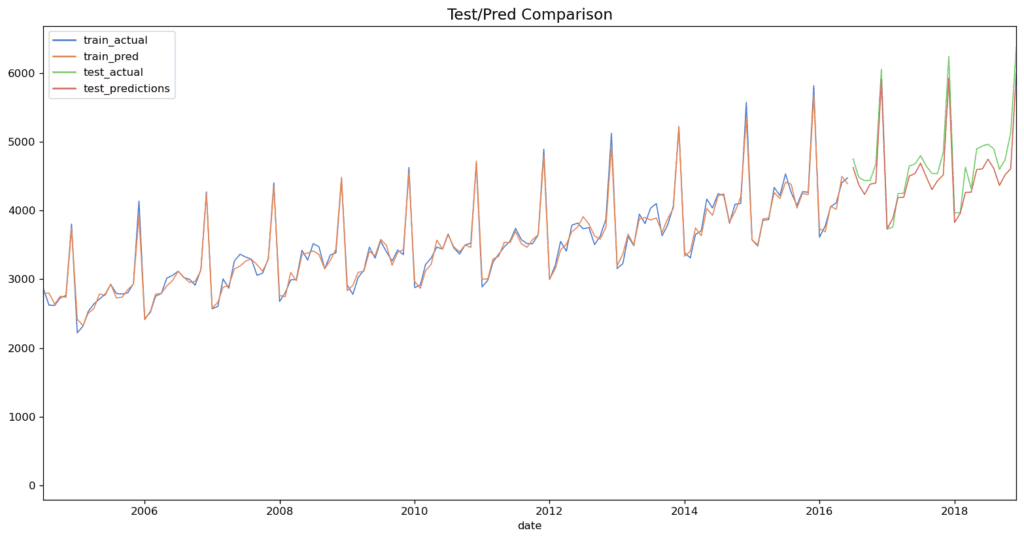
As shown above, our model’s forecast continues the seasonal pattern of the beer sales time series. On the one hand, this indicates that US beer sales will continue to rise and, on the other hand, that our model works just fine 🙂
Step #7 Measure the Performance of the Sales Forecasting Model
In this section, we will measure the performance of our ARIMA model. To learn more about this topic, check out this relataly article measuring regression performance.
The previous section’s simulation chart shows a few outliers among the prediction errors. Therefore, we focus our analysis on the percentage errors. Two helpful metrics are the mean absolute error (MAPE) and the mean absolute percentage error (MDAPE).
# Mean Absolute Percentage Error (MAPE)
MAPE = np.mean((np.abs(np.subtract(df_test['y_test'], df_test['y_test_pred'])/ df_test['y_test']))) * 100
print(f'Mean Absolute Percentage Error (MAPE): {np.round(MAPE, 2)} %')
# Median Absolute Percentage Error (MDAPE)
MDAPE = np.median((np.abs(np.subtract(df_test['y_test'], df_test['y_test_pred'])/ df_test['y_test'])) ) * 100
print(f'Median Absolute Percentage Error (MDAPE): {np.round(MDAPE, 2)} %')Mean Absolute Percentage Error (MAPE): 3.94 % Median Absolute Percentage Error (MDAPE): 3.49 %
The percent errors show that our ARIMA model achieves a decent predictive performance.
Summary
This Python tutorial has shown how to use SARIMA for sales forecasting. Sales forecasting is important for businesses because it can help them to make informed decisions about production, inventory management, and staffing, among other things. By accurately forecasting sales, businesses can ensure that they have the right amount of product available to meet customer sales, avoid overproduction and excess inventory, and plan for future growth. The use cases presented were forecasting beer sales, and we have used arima to analyze seasonal sales data.
In the first part, we have learned how ARIMA works, what Stationarity is and how to check if a time series is stationary. In the second part, we developed an ARIMA model in Python to create a forecast for US beer sales. For this purpose, we created an in-sample forecast and used Auto-tARIMA to find the optimal parameters for our sales forecasting model.
If you have any questions or suggestions, please let me know in the comments, and I will do my best to answer.

Sources and Further Reading
- Charu C. Aggarwal (2018) Neural Networks and Deep Learning
- Jansen (2020) Machine Learning for Algorithmic Trading: Predictive models to extract signals from market and alternative data for systematic trading strategies with Python
- Aurélien Géron (2019) Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems
- David Forsyth (2019) Applied Machine Learning Springer
- Andriy Burkov (2020) Machine Learning Engineering
The links above to Amazon are affiliate links. By buying through these links, you support the Relataly.com blog and help to cover the hosting costs. Using the links does not affect the price.
Want to learn more about time series analysis and prediction?
Check out these recent relataly tutorials:
- Stock Market Prediction – Building a Univariate Model using Keras Recurrent Neural Networks in Python.
- Building Multivariate Time Series Models for Stock Market Prediction with Python
- Time Series Forecasting – Creating a Multi-Step Forecast in Python
- Python Cheat Sheet: Measuring Prediction Errors in Time Series Forecasting
- Evaluate Time Series Forecasting Models with Python
Hi Florian,
This is great stuff!
One question, how would one put the confidence interval on the graph?